[Paper Review] Unsupervised Deep Embedding for Clustering Analysis
거꾸로 읽는 self-supervised learning의 첫 번째 논문
본 논문은 2016년 PMLR에 실렸으며 이미지 및 텍스트 분류에서, feature representations과 clustering을 동시에 학습하기 위해 Deep Embedded Clustering(DEC)을 제안하였습니다.
Overview
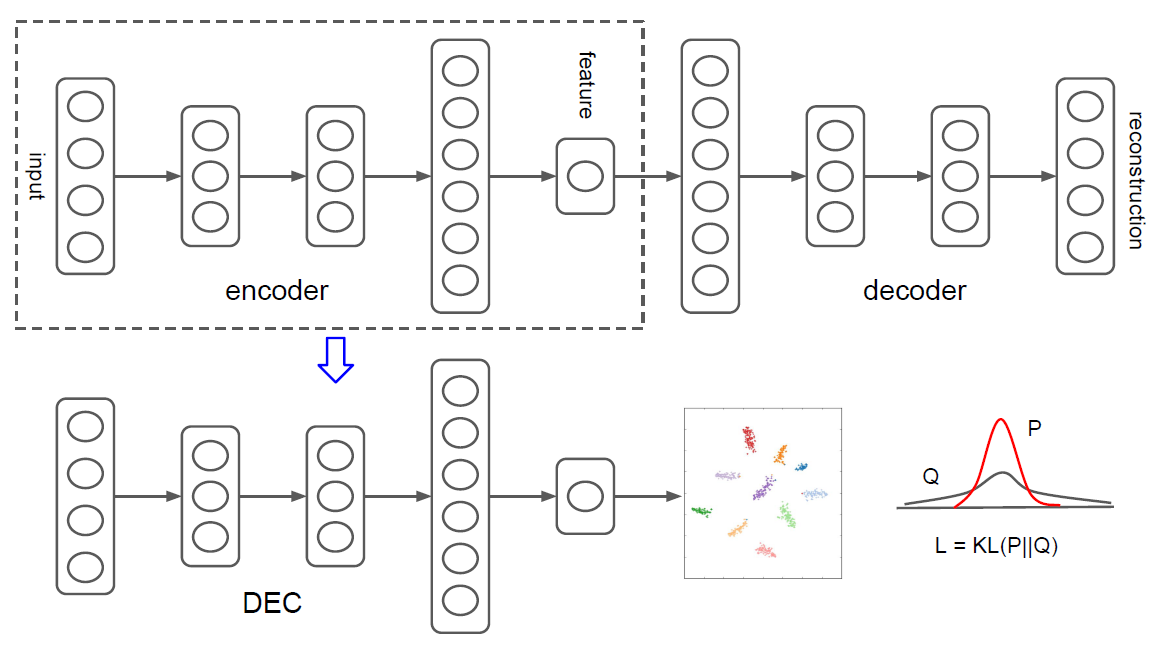
네트워크 구조
- Pretrain (Initialization phase)
- Model: 각 layer가 denoising autoencoder로 이루어진 stacked autoencoder(SAE)
- Loss: Reconstruction loss
- Task: Encoder는 한 번에 한 층씩 학습(greedy layer-wise training) + Encoder에 Decoder를 연결하여 input을 재구성(reconstruction)하도록 학습 \(\rightarrow\) Reconstruction loss 최소화
- Finetune
- Model: SAE의 encoder
- Loss: KL-Divergence loss \(\rightarrow\) Q(발생 확률 분포)와 P(타켓 분포)의 차이
- Task: Data space에서 feature space로 Mapping + Clustering \(\rightarrow\) KL-Divergence loss 최소화
- Contribution: Unsupervised learning 알고리즘인 클러스터링을 supervised learning처럼 학습 가능
Introduction
클러스터링(clustering)은 데이터 분석 및 시각화(visualization)에서 핵심적인 기법이며, unsupervised machine learning의 알고리즘으로써 널리 연구되었습니다. 클러스터링 알고리즘은 feature space에서 데이터를 표현하기 위해 distance(또는 dissimilarity)를 사용합니다. 대표적으로 k-means 클러스터링 알고리즘은 Euclidean distance를 사용하여 feature space의 point들 간의 거리를 측정합니다. 이처럼 distance는 클러스터링 알고리즘에서 중요한 역할을 합니다. 그러나 feature space의 선택 또한 중요합니다. 이미지 데이터의 경우 여러 픽셀이 모여 하나의 이미지를 나타내기 때문에, feature space를 단순하게 raw pixels의 벡터로 두고 Euclidian distance를 사용하여 픽셀 간 거리를 비교하는 것은 비효율적입니다.
결국 저자들은 다음과 같은 의문에 도달하였습니다. “feature space의 학습과 clustering을 동시에 해결할 수는 없을까?” 본 연구에서는 현재의 soft cluster assignment에서 도출된 보조 타겟 분포(auxiliary target distribution)를 사용하여 clusters를 재정의하는 방법을 제안하였습니다. 이를 통해 clustering 및 feautre representation을 개선하였습니다. 이 실험은 이미지와 텍스트 데이터셋에서 정확도와 running time 모두 최신의 클러스터링 기법들보다 향상된 성능을 보였습니다. 또한 DEC는 hyperparameters 선택에 있어서도 훨씬 덜 민감했습니다.
Contributions
- Deep embedding과 clustering을 동시에 최적화
- Soft assignment를 통한 clusters 재정의
- 정확도 및 속도에서 SOTA clustering 달성
Deep embeddded clustering
먼저 non-linear mapping \(f_\theta\)를 사용하여 data space X에 있는 data를 latent feature space Z로 변환하였습니다. Z의 차원은 “curse of dimensionality”를 피하기 위해 X 보다 작아야 했습니다. 본 연구에서 제안하는 DEC 알고리즘은 data를 X에서 Z로 mapping하는 DNN의 파라미터 θ를 학습하면서, 동시에 feature space Z의 cluter center {\(\mu _j \in Z\)}\(_{j=1}^k\)를 학습하여 데이터 클러스터링 하였습니다.
Deep embedded clustering은 두 단계로 이루어져 있습니다.
- Parameter initialization with a deep autoencoder
- Parameter optimization (i.e., clustering)
- 보조 타겟 분포(auxiliary target distribution)를 계산하고 Kullback-Leibler divergence를 최소화하는 것을 반복하여 최적화합니다.
논문의 다음 순서는 “Clustering with KL divergence”이지만, 원활한 설명을 위하여 “Parameter initialization” 먼저 작성하겠습니다.
Parameter initialization
DNN parameters θ와 cluster centroids {\(\mu _j\)}의 초기화 방법을 알아보겠습니다.
DEC network의 θ는 Stacked autoencoder(SAE)를 사용하여 초기화하였습니다. 또한, SAE의 초기화를 위해 random corruption 이후 이전 계층의 츨력을 재구성하도록 학습된 denoising autoencoder(DA)가 활용되었습니다. 즉 SAE의 각 레이어는 초기화된 DA로 구성되며, DA는 다음과 같이 2개의 layer로 이루어져 있습니다. \[\begin{align} \tilde{x} \sim Dropout(x) \\ h = g_1(W_1\tilde{x} + b_1) \\ \tilde{h} \sim Dropout(h) \\ y = g_2(W_2\tilde{h} + b_2) \end{align}\]
SAE는 여러 개의 히든 레이어를 가지는 오토인코더이며, 레이어를 추가할수록 오토인코더가 더 복잡한 인코딩(부호화)을 학습할 수 있게 됩니다. DA는 입력에 noise를 추가하고 noise가 없는 원본 입력을 재구성하도록 학습하는 방법입니다. Stacked autoencoder 및 denoising autoencoder를 포함하여 autoencoder에 대한 자세한 설명은 Excelsior-JH님의 오토인코더 (AutoEncoder)를 참고하시길 바랍니다.
DA는 least squares loss \(\Vert x-y \Vert^2\)을 최소화하도록 학습합니다. DA의 하나의 layer를 학습한 후, output h를 input으로 사용하여 다음 layer를 학습하며 진행됩니다. 이러한 greedy layer-wise training 이후 reverse layer-wise training 순서로, encoder layers와 decoder layers를 붙여서 deep autoencoder를 형성하고 다음으로 재구성 손실(reconstruction loss)를 최소화하도록 학습합니다. SAE는 중간에 bottleneck coding layer가 있는 multilayer deep autoencoder가 됩니다.

네트워크 구조
최종적으로 SAE의 decoder layers를 버리고 encoder layers를 data space와 feature space 간의 initial mapping으로 사용합니다. Cluster centers를 초기화하기 위해 데이터를 초기화된 DNN에 넣어 embedded data를 얻고 feature space Z에서 k-means clustering하여 k개의 initial centroids \(\lbrace\mu _j\rbrace_{j=1}^k\)를 얻습니다.
Clustering with KL divergence
Non-linear mapping \(f_\theta\)과 cluster centroids {\(\mu _j\)}\(_{j=1}^k\)의 초기값을 추정하였으므로, 비지도 알고리즘을 사용하여 clustering을 개선하는 방법을 살펴보겠습니다.
KL divergence 기반 clustering은 다음의 두 단계를 반복하며 최적화합니다.
Step 1. X \(\rightarrow\) Z로 mapping된 embedded points와 cluster centroids 간의 soft assignment를 계산합니다.
\(\Rightarrow\) Embedded points와 cluster centroids 간의 거리를 계산하여, Embedded point가 cluster에 속할 확률(soft assignment)를 구하는 것입니다.
Step 2. Deep mapping \(f_θ\)을 업데이트하고 보조 타겟 분포(auxiliary target distribution)를 통해 높은 신뢰도(high confidence)로 학습하여 cluster centroids를 재정의합니다.
\(\Rightarrow\) 보조 타겟 분포를 label로 사용함으로써, unsupervised learning 알고리즘인 클러스터링이 마치 supervised learning처럼 학습되어 높은 신뢰도로 학습한다고 말할 수 있습니다.
수렴 기준에 충족될 때까지 이 절차를 반복합니다.
SOFT ASSIGNMENT
Embedded points \(z_i\)와 cluster centroids \(\mu _j\) 간의 거리 즉, 유사도를 구하기 위해 t-분포(Studetnt’s t-distribution)를 사용하였습니다. \[q_{ij} = \frac{(1 + \lVert z_i - \mu _{j} \rVert ^2 / \alpha)^{-\frac{\alpha+1}{2}}} {\sum _{j'}(1 + \lVert z_i - \mu _{j'} \rVert ^2 / \alpha)^{-\frac{\alpha+1}{2}}}\]
\(\alpha\)는 t-분포의 자유도(degree of freedom)를 나타내며, \(q_{ij}\)는 sample i가 cluster j에 속할 확률(i.e., soft assignment)을 나타냅니다. Clustering은 비지도 알고리즘으로써 alpha를 validation set에 cross-validate하지 못하므로 모든 실험에서 alpha를 1로 설정하였습니다.
[참고] \(q_{ij}\)는 어떻게 도출되었을까?
t-분포의 공식은 다음과 같습니다. \[f(t) = \frac{\varGamma(\frac{\alpha+1}{2})}{\sqrt{\alpha\pi}\varGamma(\frac{\alpha}{2})}(1+\frac{t^2}{\alpha})^{-\frac{\alpha+1}{2}}\]
t-분포를 논문에 맞게 적용해보자면, 데이터 t는 두 점 사이의 거리 \(\Vert z_i - \mu _j\Vert\)가 되며 식은 다음과 같이 정리됩니다. \[\begin{aligned} q_{ij} &= \frac{\frac{\varGamma(\frac{\alpha+1}{2})}{\sqrt{\alpha\pi}\varGamma(\frac{\alpha}{2})}(1+\frac{||z_i - \mu _j||^2}{\alpha})^{-\frac{\alpha+1}{2}}}{\sum_{j'} \frac{\varGamma(\frac{\alpha+1}{2})}{\sqrt{\alpha\pi}\varGamma(\frac{\alpha}{2})}(1+\frac{\Vert z_i - \mu _{j'}\Vert^2}{\alpha})^{-\frac{\alpha+1}{2}}} \\[2em] &= \frac{\frac{\varGamma(\frac{\alpha+1}{2})}{\sqrt{\alpha\pi}\varGamma(\frac{\alpha}{2})}(1+\frac{\Vert z_i - \mu _j \Vert ^2}{\alpha})^{-\frac{\alpha+1}{2}}} {\frac{\varGamma(\frac{\alpha+1}{2})}{\sqrt{\alpha\pi}\varGamma(\frac{\alpha}{2})}\sum_{j'}(1+\frac{\Vert z_i - \mu _{j'} \Vert^2}{\alpha})^{-\frac{\alpha+1}{2}}} \\[2em] &= \frac{(1+\frac{\Vert z_i - \mu _j \Vert^2}{\alpha})^{-\frac{\alpha+1}{2}}}{\sum_{j'}(1+\frac{\Vert z_i - \mu _{j'} \Vert^2}{\alpha})^{-\frac{\alpha+1}{2}}} \\[2em] \end{aligned}\]
또한, alpha = 1로 설정하였으므로 최종적으로 다음과 같은 식을 얻을 수 있습니다. \[q_{ij} = \frac{(1 + \lVert z_i - \mu _{j} \rVert ^2)^{-1}} {\sum _{j'}(1 + \lVert z_i - \mu _{j'} \rVert ^2)^{-1}}\]
분모는 L1 정규화(L1-normalization)를 적용한 것으로, 각 벡터 안의 요소 값을 모두 더한 것이 크기가 1이 되도록 벡터들의 크기를 조절하였습니다.
따라서, \(q_{ij}\)는 sample i가 cluster j에 속할 확률이 되는 것입니다.
예를 들어 \(\Vert z_i - \mu _j \Vert^2\)가 0.1일 때는 sample과 cluster centroid가 가까울 것이고, 10일 때는 비교적 멀 것입니다. 이 때의 cluster에 속할 확률 \(q_{ij}\)는 각각 약 0.92, 0.01이 되겠지요.
KL DIVERGENCE MINIMIZATION
\(q_{ij}\)를 통해 보조 타겟 분포(auxiliary target distribution)를 구하고, 이를 label로 사용하여 높은 신뢰도(high confidence)로 학습하면서 clusters를 재정의하였습니다.
기존의 클러스터링은 unsupervised learning으로 사용되었지만, 본 논문에서는 보조 타겟 분포를 label로 사용하여 마치 supervised learning처럼 학습하였으므로 높은 신뢰도(high confidence)로 clusters를 재정의했다고 할 수 있습니다.
구체적으로 DEC는 soft assignments를 target distribution에 매칭하면서 학습합니다. Soft assignments \(q_{ij}\)와 target distribution \(p_{ij}\) 간의 KL divergence loss를 목적함수로 정의하여, 두 분포의 차이를 최소화하도록 학습하였습니다. \[L = KL(P||Q) = \sum_i\sum_jp_{ij}\log\frac{p_{ij}}{q_{ij}}\]
[참고] KL DIVERGENCE에 대한 설명
KL divergence(Kullback-Leibler divergence, KLD)는 두 확률분포의 차이를 계산하는데에 사용되는 함수입니다. 두 확률변수에 대한 확률분포 P, Q가 있을 때, 두 분포의 KLD는 다음과 같이 정의할 수 있습니다. \[D_{KL}(P\Vert Q) = \sum_i P(i)\log \frac{P(i)}{Q(i)}\]
텐서플로우 공식 문서에 정의되어 있는 용어로 설명해보자면, KLD는 y_true(P)가 가지는 분포값과 y_pred(Q)가 가지는 분포값이 얼마나 다른 지를 확인하는 방법입니다. KLD의 값이 낮을수록 두 분포가 유사하다고 해석합니다. KLD에 대한 자세한 설명은 대학원생이 쉽게 설명해보기의 KL-Divergence Loss 간단 설명과 Easy is Perfect의 엔트로피(Entropy)와 크로스 엔트로피(Cross-Entropy)의 쉬운 개념 설명를 참고하시길 바랍니다. \[\begin{aligned} D_{KL}(P \Vert Q) &= H(P,Q) - H(P) \\ &= (\sum_x p(x) \log q(x)) - (-\sum_x p(x) \log p(x)) \\ \end{aligned}\]
- H(P, Q): P 대신 Q를 사용할 때의 cross-entropy
- H(P): 원래의 P 분포가 가지는 entropy
따라서, 본 연구에서는 두 분포 soft assignments \(q_{ij}\)와 target distribution \(p_{ij}\)의 차이를 최소화하는 방향으로 학습한다는 것을 알 수 있습니다.
다음으로, target distibutions P를 구하는 것은 DEC의 성능에 있어서 중요한 요소로 작용합니다. \(q_i\)는 진짜 label이 아닌 unsupervised setting으로 계산된 확률이므로 \(p_i\)역시 softer probabilistic targets을 사용하는 것이 자연스럽다고 합니다.
특히 저자들은 타겟 분포(target distribution)가 다음과 같은 특징을 갖도록 수식을 구성하였습니다.
- 클러스터 내 순도(purity) 증가
- 높은 신뢰도(high confidence)로 할당된 data points에 더 강조
- 대형 클러스터(large cluster)가 hidden feature space를 왜곡하는 것을 방지하기 위해 각 centroid의 loss contributions을 정규화
따라서 보조 타겟 분포(auxiliary target distribution)는 다음과 같이 정의됩니다. \[p_{ij} = \frac{q_{ij}^2 / f_j}{\sum_{j'}q_{ij'}^2 / f_{j'}}\]
\(f_j = \sum _i q_{ij}\)로, sample i가 cluster j에 속할 확률들의 합을 나타냅니다.
학습 전략은 self-training의 형태로 볼 수 있습니다. Self-training에서 initial classifier와 unlabeled dataset을 사용한 다음, 스스로 높은 신뢰도의 예측을 학습하기 위해 initial classifier로 unlabeled dataset에 label을 지정합니다. 실제로 실험에서 DEC는 높은 신뢰도의 예측에서 학습하여 반복할수록 초기 추정치를 개선하였고, 이는 낮은 신뢰도의 예측을 개선하는 데 도움이 되었다고 합니다.
보조 타겟 분포를 label로 사용하여 self-training한다는 점에서 self-supervised learning이라고 할 수 있습니다.
[참고] \(p_{ij}\)는 어떻게 도출되었을까?
본 논문에서는 \(p_{ij}\)의 도출에 대한 자세한 설명이 없기에 추론해 보았습니다.
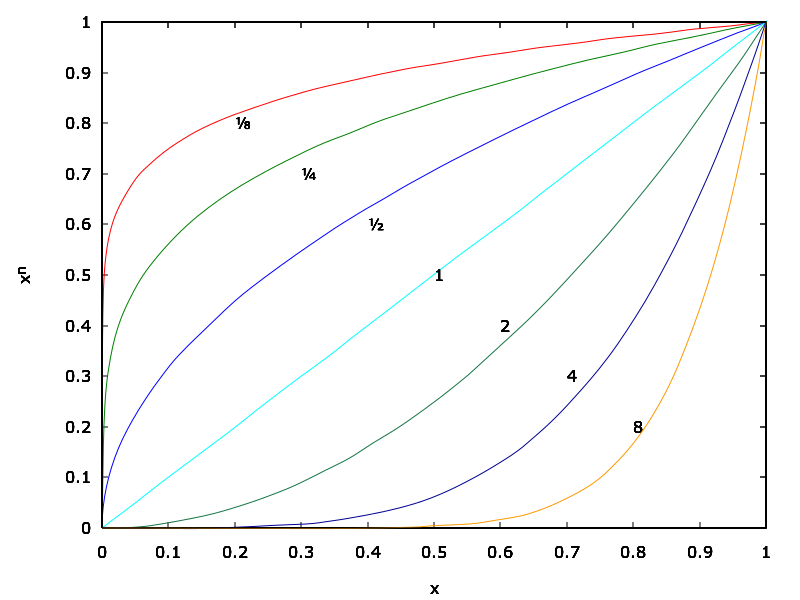
거듭제곱 함수 그래프(출처: Wikipedia)
\(q_{ij}\)에 제곱을 취할 경우 모든 데이터의 값이 기존보다 작아지지만, \(x^2\) 그래프의 감소 폭을 보면 기존 값이 작을 경우 더욱 작아지게 됩니다.
\(q_{ij}\)에 제곱을 취함으로써 기존의 높은 확률 값(= 높은 신뢰도의 예측)은 크게 변하지 않지만, 낮은 신뢰도의 예측은 더 크게 낮아지게 되는거죠.
Ex) \(q_{11} = 0.96, q_{31} = 0.02 \rightarrow {q_{11}}^2 = 0.9216, {q_{31}}^2 = 0.0004\)
원활한 이해를 위하여 간단한 예시를 통해 \(p_{ij}\)의 도출 과정을 직접 확인해보겠습니다.
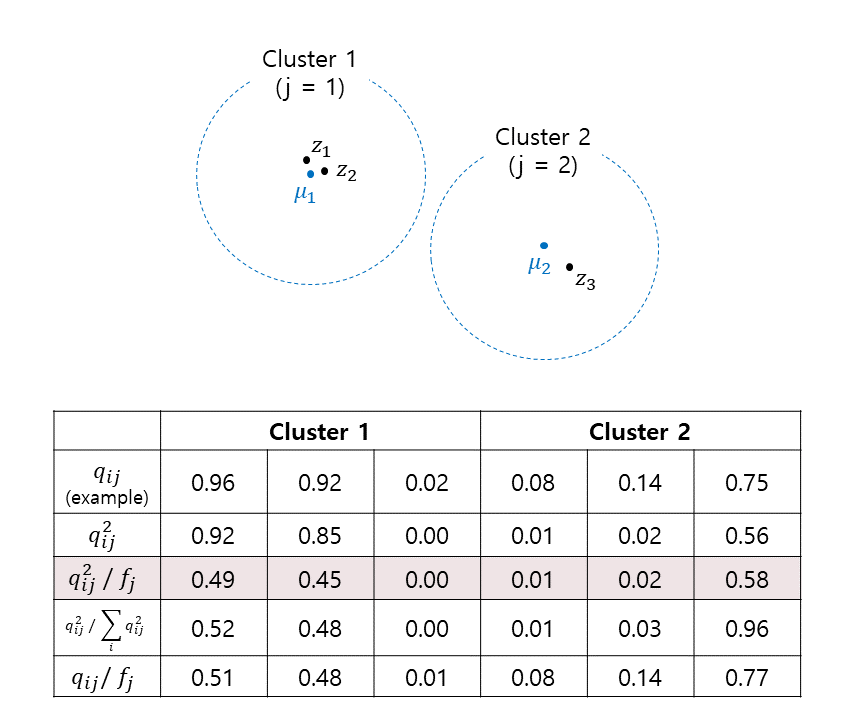
- \(z_i\): Embedded points (Data space X에서 feature space Z로 mapping된 데이터)
- \(\mu _j\): Cluster j의 중심(Cluster centroid)
- \(q_{ij}\): \(z_i\)가 cluster j에 속할 확률
- \(f_j\): \(\sum _i q_{ij}\) (Cluster j의 모든 \(q_{ij}\)의 합)
(a) \(q_{ij}\): Embedded points \(z_{i}\)에 대한 \(q_{ij}\)를 가정해보겠습니다.
(b) \(q_{ij}^2\): 제곱으로 인해 높은 \(q_{ij}\) 대비 낮은 \(q_{ij}\)가 더 작아지므로 높은 신뢰도의 예측과 낮은 신뢰도의 예측 간의 격차가 벌어집니다.
(c) \(q_{ij}^2 / f_j\): \(q_{ij}^2\)을 그대로 사용하면 large cluster(위의 예시에서 cluster 1)의 값이 너무 커지므로 \(f_j\)로 정규화(normalization)를 합니다. Clusters 간의 크기를 맞추기 위한 정규화로 보시며 됩니다.
(d) \(q_{ij}^2 / \sum _i q_{ij}^2\): 번외로 \(\sum _i q_{ij}^2\)가 아닌 \(\sum _i q_{ij}\)으로 정규화한 이유를 보자면, \(q_{32}\)의 경우 \(\sum _i q_{ij}^2\)로 정규화 했을 때 기존의 예측값 \(q_{ij}\)보다 커진 것을 확인하실 수 있습니다. 이 부분에 경우 직접 숫자를 대입해보고 이해하였기에 혹시 수식적으로 안되는 이유를 아신다면 댓글 또는 메일 주시면 감사하겠습니다.
(e) \(q_{ij} / \sum _i q_{ij}\): 번외로 보자면, 높은 신뢰도의 예측에 강조하지도 못하고, clusters 간의 정규화만 되어 절대 사용하면 안 될 것 같습니다.
정리하자면, 저자들이 희망하는 타겟 분포의 특징은 다음과 같았습니다.
1.클러스터 내 순도 증가 \(\Rightarrow\) (b) Sample i가 cluster j에 속할 확률인 예측값 \(q_{ij}\) 강조
- 높은 신뢰도(high confidence)로 할당된 data points에 더 강조
\(\Rightarrow\) (b) 1번과 동일한 맥락
높은 신뢰도의 예측이란 높은 값의 \(q_{ij}\), 낮은 신뢰도의 예측이란 낮은 값의 \(q_{ij}\)
즉, 낮은 값의 \(q_{ij}\) 대비 높은 값의 \(q_{ij}\)에 더욱 강조 - Large cluster가 hidden feature space를 왜곡하는 것을 방지하기 위해 각 centroid의 loss contributions을 정규화
\(\Rightarrow\) (c) 기본적으로 large cluster란, cluster안에 속하는 embedded points \(z_i\)가 많은 클러스터입니다. 그러나 \(q_{ij}\)의 수식에 따르면 \(q_{ij}\)는 0이 될 수 없으므로, 각 cluster j는 모두 동일한 개수의 \(q_{ij}\)를 갖게 됩니다.
따라서 본 연구에서 말하는 large cluster란 \(\sum _i q_{ij}\)의 값이 높은 cluster가 됩니다.
마지막으로 분모는 앞서 언급하였듯이 L1-normalization으로 생각하시면 됩니다.
OPTIMIZATION
Momentum과 함께 Stochastic Gradient Descent (SGD)를 사용하여 cluster centers {\(\mu _j\)}와 DNN parameters \(\theta\)를 동시에 최적화합니다. 각 데이터 points \(z_i\)와 각 cluster centroid \(\mu _j\)의 feature embedding에 대한 gradients \(L\)은 다음과 같이 계산됩니다. \[\begin{align} \frac{\partial L}{\partial z_i} = \frac{\alpha + 1}{\alpha}\sum _j{(1 + \frac{\Vert z_i - \mu _j \Vert^2}{\alpha})}^{-1} \times (p_{ij} - q_{ij})(z_i - \mu _j) \\ \frac{\partial L}{\partial \mu _i} = - \frac{\alpha + 1}{\alpha}\sum _j{(1 + \frac{\Vert z_i - \mu _j \Vert^2}{\alpha})}^{-1} \times (p_{ij} - q_{ij})(z_i - \mu _j) \end{align}\]
Experiments
Datasets
1개의 텍스트 데이터셋 “REUTERS”와 2개의 이미지 데이터셋 “MNIST” 및 “STL-10”에 대하여 성능을 평가하였습니다.
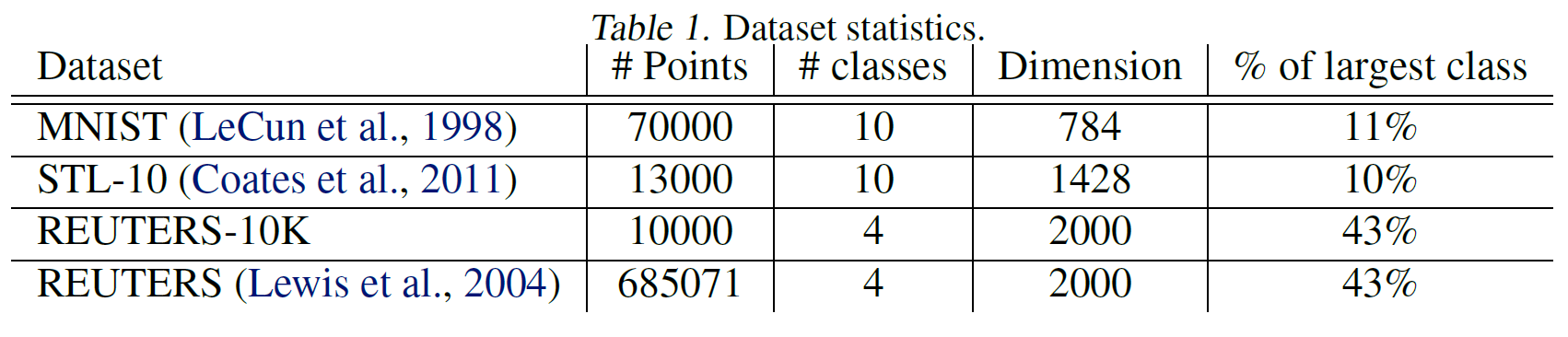
본 연구에서 사용된 데이터셋의 정보
Evaluation Metric
다른 알고리즘과 평가 및 비교하기 위하여 standard unsupervisd evaluation metric 및 procols을 사용하였습니다. 모든 알고리즘에서 clusters의 개수를 ground-truth 카테고리의 개수로 설정하고 unsupervised clustering accuracy(ACC)로 성능을 평가하였습니다. \[ACC = \displaystyle\max _m\frac{\sum_{i=1}^{n} 1\lbrace l_i = m(c_i)\rbrace}{n}\]
- \(l_i\): Ground-truth label
- \(c_i\): 알고리즘으로 할당된 cluster
- \(m\): Clusters와 labels 간의 가능한 모든 일대일 mapping
직관적으로 metric은 unsupervised algorithm과 ground truth에서 클러스터 할당(cluster assignments)를 가져온 다음 이들 간의 최고의 매칭을 찾습니다.
Experiment results
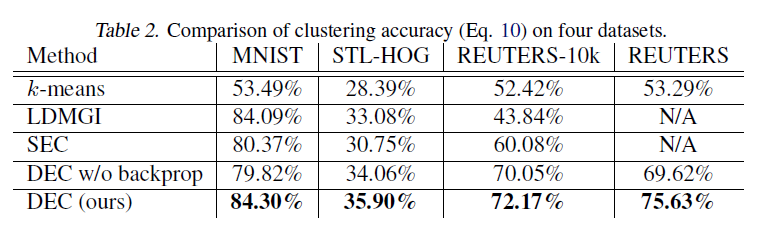
클러스터링 정확도 비교
DEC는 다른 모든 방법보다 우수한 성능을 보였습니다. LDGMI과 SEC는 스펙트럴 클러스터링(spectral clustering)으로 데이터들 간의 상대적인 관계나 연결을 중요한 정보로 사용하는 그래프 기반 클러스터링입니다. 또한, 본 연구는 end-to-end 학습의 효율성을 입증하기 위해, 클러스터링 중에 non-linear mapping \(f_\theta\)를 frezezing 즉 고정한 결과(DEC w/o backprop)도 보여주었습니다. DEC w/o backprop는 일반적으로 DEC보다 낮은 성능을 보였습니다.
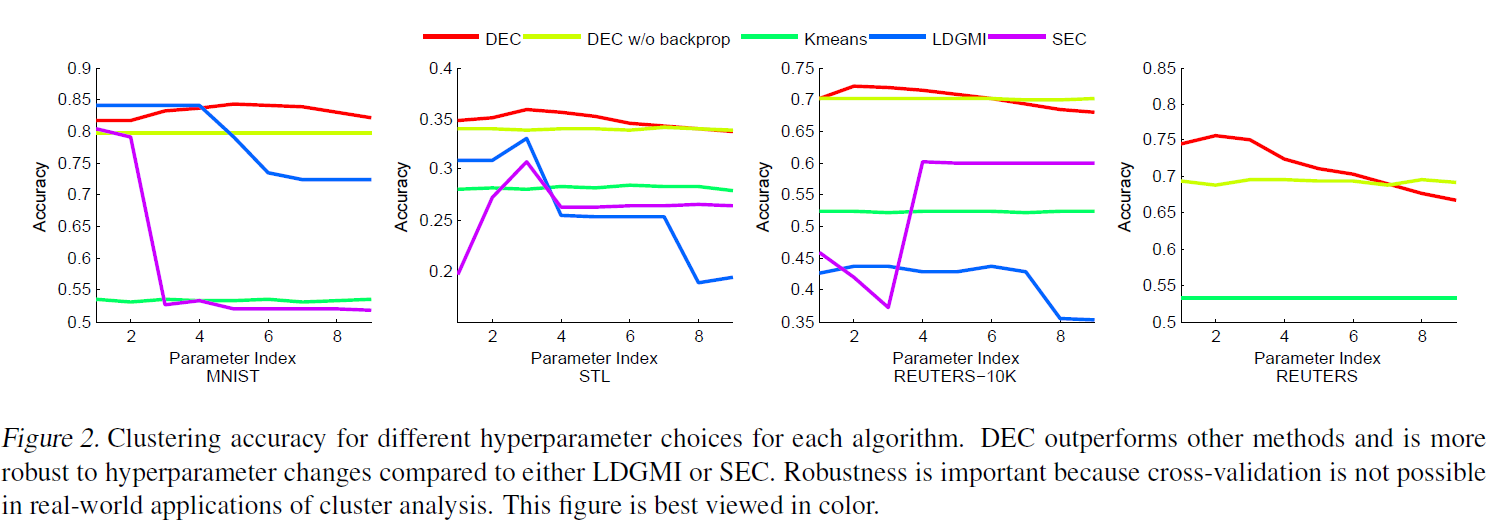
클러스터링 정확도 비교
DEC는 LDGMI과 SEC보다 하이퍼파라미터(hyperparameter)에 강건함을 보였습니다. DEC는 모든 데이터셋에서 하이퍼파라미터 \(\lambda = 40\)일 때 거의 최적의 성능을 보인 반면, 다른 알고리즘들은 다양했습니다. 또한, DEC는 GPU 가속을 사용하여 30분 만에 REUTERS 데이터셋 전체를 처리할 수 있었지만, 두 번째로 우수한 알고리즘은 LDGMI과 SEC는 수개월의 계산시간과 테라바이트의 메모리가 필요했습니다.

클러스터링 이미지
MNIST와 STL의 각 클러스터에서 10개의 최고 점수 이미지입니다. 각 y축은 cluster이며 x축의 왼쪽부터 cluster에 가장 가까운 순서대로 나열되었습니다. MNIST의 경우 DEC의 클러스터 할당은 혼란스러운 4와 9를 제외하고는 자연 클러스터와 매우 잘 일치하는 반면 STL의 경우 DEC는 비행기, 트럭 및 자동차에 대해 대부분 정확하지만 동물 사진에서는 카테고리 대신 포즈에 주의를 기울이는 것을 확인하실 수 있습니다.
Discussion
Assumptions and Objective
DEC의 기본 가정은 initial classifier의 높은 신뢰도 예측은 대부분 정확하다는 것입니다. 이 가정이 본 연구의 task에 적용되고 P의 선택이 원하는 속성을 갖는다는 것을 확인하기 위해, 각 embedded point에 대한 gradient L의 크기(magnitude) 즉 \(\lvert \partial L / \partial z_i \rvert\)를 soft assignment \(q_{ij}\)에 따라 시각화하였습니다.
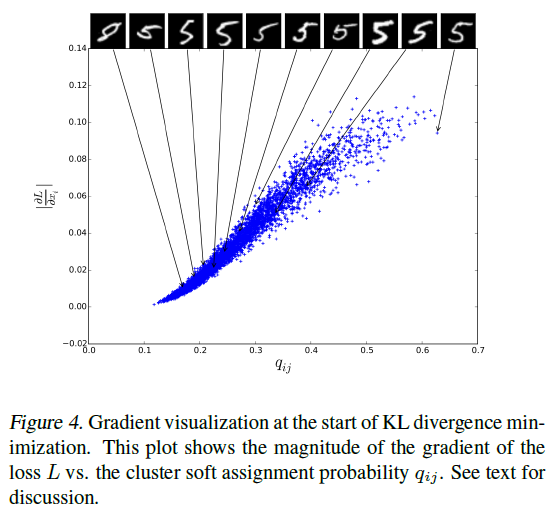
기울기 시각화
Cluter center에 더 가까운 points(큰 \(q_{ij}\))가 gradient에 더 많이 기여하는 것을 확인할 수 있습니다. 또한, \(q_{ij}\) 정렬의 각 10% 지점마다 원본 이미지를 표시하였습니다. 신뢰도가 감소할수록, instances는 더욱 모호해졌으며 결국 8로 잘못 레이블링하였습니다.
Contribution of Iterative Optimization
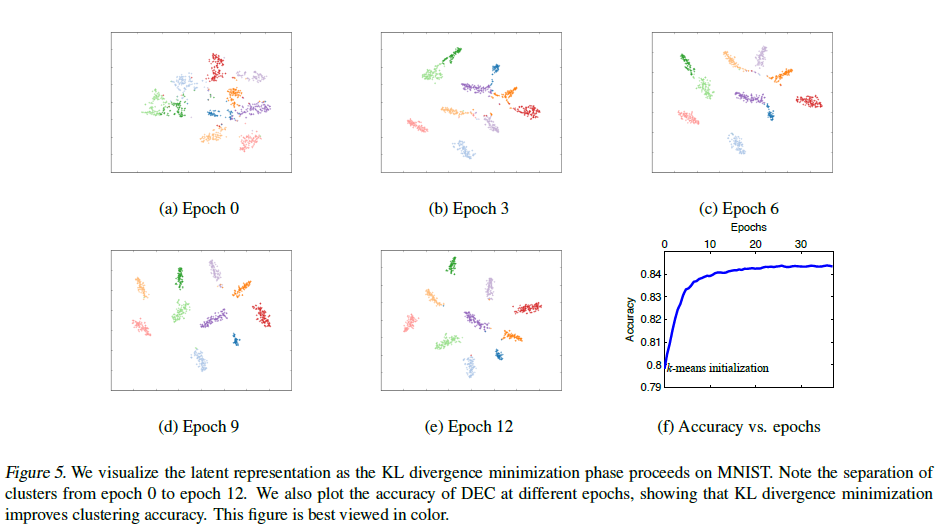
클러스터링 정확도 비교
Embedded representation을 t-SNE를 사용하여 시각화하였습니다. Cluster가 점점 더 잘 분리되는 것을 알 수 있습니다. 상단의 그림은 SGD epochs에 따라 정확도가 어떻게 개선되는 지를 나타냅니다.
Contribution of Autoencoder Initialization
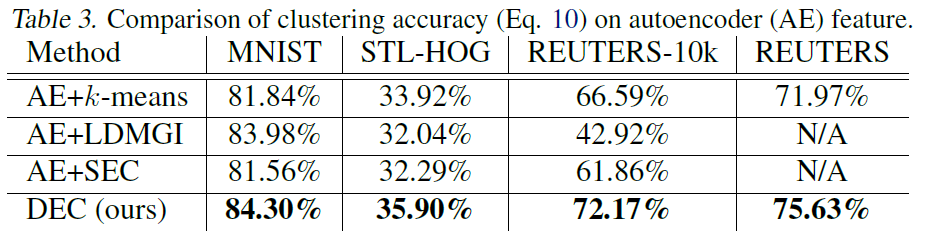
Autoencoder feature에 따른 클러스터링 정확도 비교
Autoencoder의 feature를 알고리즘에 적용한 성능을 나타냅니다. SEC 및 LDMGI의 성능은 autoencoder feature에 크게 변경되지 않는 반면, k-means은 개선되었지만 여전히 DEC보다 낮았습니다. 이는 deep embedding의 중요성과 KL divergence objective로 fine-tuning하는 것의 이점을 보여줍니다.
Performace on Imbalanced Data
불균형 데이터의 영향을 확인하기 위해, 다양한 보유율로 MNIST의 하위집합을 샘플링하였습니다. 최소 보유율 \(r_{min}\)의 경우 class 0의 데이터 개수는 확률 \(r_{min}\)만큼 유지되고 class 9의 데이터 개수는 확률 1 즉 기존 데이터 개수만큼 보유하게 되며, 다른 class들은 그 사이에 선형으로 유지됩니다. 결과적으로 가장 큰 클러스터(class 9)는 가장 작은 클러스터(class 0)의 \(1/r_{min}\)배가 됩니다.
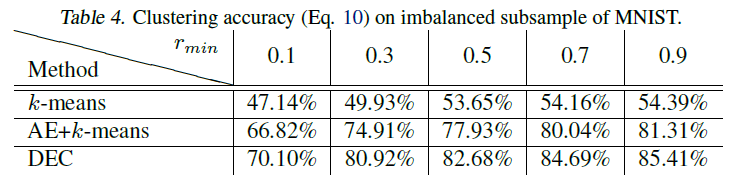
MNIST의 불균형 subsample에서의 클러스터링 정확도
표는 DEC의 클러스터의 크기 변동에 대한 강인함을 나타냅니다. 또한 DEC의 KL divergence 최소화는 autoencoder 및 k-means initialization (AE+k-means) 이후에도 클러스터링 정확도를 지속적으로 향상시키는 것을 알 수 있습니다.
Number of Clusters
지금까지는 알고리즘 간의 비교를 단순화하기 위해 클러스터 수가 주어졌다고 가정하였습니다. 그러나, 실제로는 클러스터의 수를 알 수 없는 경우가 많기에 최적의 클러스터 수를 결정해야 합니다. 이를 위해 본 연구에서는 2가지의 metrics를 정의하였습니다.
1.Standard metric: Normalizaed Mutual Information (NMI) \[NMI(l,c) = \frac{I(l,c)}{\frac{1}{2}[H(l)+H(c)]}\]
- \(l\): Ground-truth label
- \(c\): 알고리즘으로 할당된 cluster
- \(I\): 상호정보량(information metric)
- \(H\): Entropy
서로 다른 클러스터의 수로 클러스터링의 결과를 평가하기 위해 사용됩니다.
2.Generalizability \[G = \frac{L_{train}}{L_{validation}}\]
G는 training loss와 validation loss 간의 비율로 정의됩니다. Training loss가 validation loss보다 작을 때 G도 작아지며, 이는 과적합을 나타냅니다.
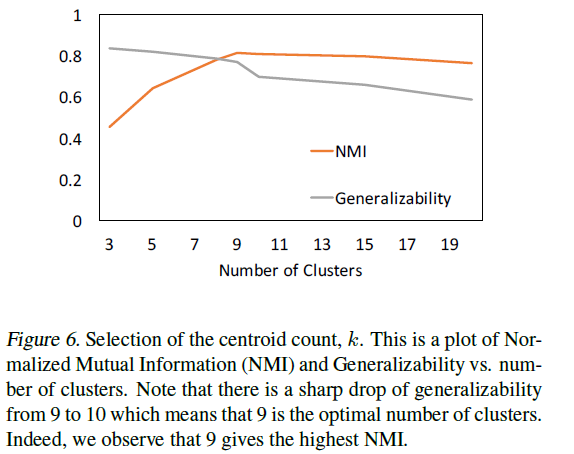
클러스터의 수 선택
클러스터 수가 9~10으로 증가할 때 일반화가능성(generalizability)는 크게 떨어지며, 9가 최적의 클러스터 수라는 것을 나타냅니다. NMI 점수도 9에서 가장 높았으며, 이를 통해 일반화가능성이 클러스터의 수를 선택하는 데에 좋은 metric이라는 것을 증명합니다. MNIST 데이터셋은 총 10개의 class를 가지지만, NMI 점수는 클러스터의 수 10이 아닌 9에서 가장 높았는데요, 글을 쓸 때 9와 4가 유사하여 DEC는 하나의 클러스터로 묶어야 한다고 생각했기 때문이라고 합니다.

클러스터링 이미지
위에서 봤던 MNIST 클러스터링 그림을 보면 9와 4를 잘 분류하지 못한 것을 알 수 있습니다.
[참고] Mutual Information에 대한 설명
두 확률변수 사이의 상호정보량(mutual information, MI)은 하나의 확률변수가 다른 확률변수에 대해 제공하는 정보의 양을 의미합니다. \(I(X;Y)\)로 표현하며 다음과 같이 나타냅니다. \[\begin{align} I(X;Y) = \sum_{y \in Y} \sum_{x \in X} p(x,y)log\frac{p(x,y)}{p(x)p(y)} \end{align}\]
p(x)는 x가 일어날 확률이며, p(x,y)는 x와 y가 동시에 일어날 확률입니다. 만약 두 확률변수가 독립(independent)이라면, \(p(x,y) = p(x)p(y)\)가 되고 log 내 식의 값이 1이 되면서 MI 값은 0이 됩니다. 따라서 X, Y가 dependent할수록 MI 값은 증가합니다. 위 식에서 X와 Y의 순서를 바꾸어도 MI의 값은 동일합니다.
Conclustion
본 연구에서 제안하는 Deep Embedded Clustering, DEC는 공동으로 최적화된 feature space에서 data points를 클러스터링하는 알고리즘입니다. DEC는 self-training으로 얻은 타켓 분포를 가지고 반복적으로 KL divergence 기반 clustering objective를 최적화함으로써 학습합니다. 이런 방법은 unsupervised learning의 확장판으로 볼 수 있습니다. DEC의 프레임워크는 label 없이 클러스터링에 특화된 표현(representation)을 학습하는 방법을 제공합니다.
DEC는 좋은 성능을 보였으며 하이퍼파라미터의 세팅에 대해서도 강건하였습니다.
References
[1] Xie, Junyuan, Ross Girshick, and Ali Farhadi. “Unsupervised deep embedding for clustering analysis.” International conference on machine learning. PMLR, 2016. [Paper]
[2] 슈퍼짱짱, “[논문] DEC 리뷰: Unsupervised Deep Embedding for Clustering Analysis” [Online]