[Paper Review] Deep Adaptive Image Clustering
거꾸로 읽는 self-supervised learning의 두 번째 논문
본 논문은 2017년 ICCV에 개제되었으며
Overview
Image clustering 문제를 Binary pairwise-classification 프레임워크로 전환하여 접근
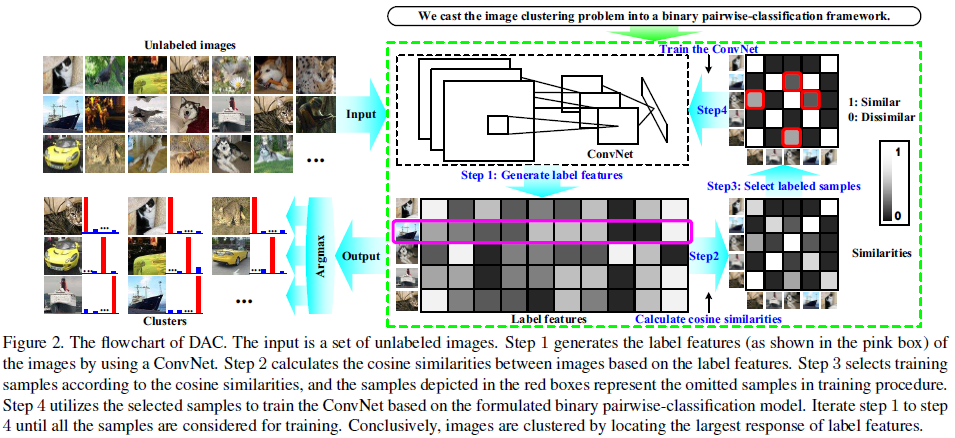
The flowchart of Deep Adaptive Clustering
- Framework:
- Step 1. Generate label features: Input인 unlabeled images를 ConvNet을 통해 label features로 변환 (즉, 이미지를 representation vectors로 변환)
- Step 2. Cacluate cosine similarities: Cosine distance로 label features 간의 유사성 추정
- Step 3. Select labeled samples: Cosine similarity를 기반으로 유사성이 모호한 데이터(상단의 그림에서 빨간 상자)는 제외하고, 값이 1인 것은 similar한 이미지 쌍으로, 값이 0인 것은 dissimilar한 이미지 쌍으로 여기며 training samples 선택
- Step 4. Train the ConvNet: 선정된 training samples로 ConvNet 학습
- Model:
- Loss:
- Task:
- Contribution:
Introduction
클러스터링 기법으로는 전통적으로 K-means 및 병합 군집(agglomerative clustering)과 같은 다양한 기법들이 연구되었습니다. 기존에는 사전 정의된 distance metrics(e.g, Euclidean Metric)를 활용하여 클러스터링하였지만, 이미지 데이터셋에서 distance 기반 척도로는 이미지간의 유사성을 구별하기 어렵다는 한계가 있습니다. (예를 들어, 이미지 픽셀 벡터를 기반으로 pixel MSE가 낮으면 같은 얼굴이고 높으면 다른 얼굴일까요? 아니죠!)
최근에는 Deep unsupervised feature learning 기법(e.g., autoencoder, auto-encoding Variational bayes)이 이미지의 표현 학습(representation learning)에서 관심을 받고 있습니다. Deep unsupervised feature learning은 multi-stage pipeline으로 형성되어 먼저 unsupervised로 deep neural networks(DNN)을 사전학습하고 후처리로써 기존의 방법으로 이미지를 클러스터링 합니다. 그러나 이러한 representation 기반 접근 방식은 multi-stage 패러다임의 번거로움과, 학습된 representation은 unsupervised feature learning 이후에 고정된다는 점에서 한계가 있습니다. 결과적으로 클러스터링 과정에서 representation은 더 이상 개선될 수 없습니다.
본 연구는 이미지 클러스터링을 위한 single-stage ConvNet 기반 방법인 Deep Adaptive Clustering(DAC)을 제안하였습니다. Image clustering task를 한 쌍의 이미지가 같은 클러스터에 속하는지 아닌지 판별하는 binary pairwise-classification 문제로 여깁니다. 구체적으로 이미지는 deep ConvNet으로 생성된 label features로 표현되고, 유사성은 label features간의 cosine distance로 측정됩니다. 또한, DAC에 제약조건을 추가하였으며 이를 통해 학습된 label feautres는 one-hot vectors가 되는 경향이 있습니다. 본 연구에서는 cosine distance로 추정된 유사성을 사용하였으며 실제 유사성은 알 수 없습니다. 따라서 모델의 최적화를 위해 alternating iterative 방법인 Adaptive Learning 알고리즘을 개발하였습니다.
During each iteration, pairwise images with the estimated similarities are first selected based on the fixed ConvNet. Subsequently, DAC employs the selected labeled samples to train the ConvNet in a supervised way. The algorithm converges when all the samples are included for training and the objective function of the binary pairwise-classification problem can not be improved further. Finally, images are clustered by locating the largest response of label features. The visual results of DAC on the MNIST test set are illustrated in Figure 1. To sum up, the main contributions of this work are:
Contributions
- DAC
Deep Adaptive Clustering Model
먼저, pairwise 이미지 간의 관계를 이진법(binary)으로 가정합니다. 즉, 각 쌍의 이미지는 같은 클러스터에 속하거나 다른 클러스터에 속합니다. 이 가정을 기반으로 image clustering task를 binary pairwise-classifiation 모델로 변환합니다.

The flowchart of DAC
Binary Pairwise-Classification for Clustering
학습 데이터를 \(D = {(x_i,x_j,r_{ij})}_{i=1,j=1}^n\)로 표현할 때 \(x_i, x_j \in X\)는 unlabeled 이미지이며, \(r_{ij} \in Y\)은 unknown binary variable입니다. \(r_{ij} = 1\)이면 \(x_i\)와 \(x_j\)가 같은 클러스터에, \(r_{ij} = 0\)이면 \(x_i\)와 \(x_j\)가 다른 클러스터에 속한다는 것을 나타냅니다.
DAC의 목적 함수(objective function)은 다음과 같이 정의됩니다. \[\min_\text{w} E(\text{w}) = \sum_{i,j} L(r_{ij},g(x_i,x_j;\text{w})), \tag{1}\]
- \(g(x_i,x_j;w)\): 추정된 유사도(estimated similarity), 즉 모델이 학습하여 추론한 \(x_i\)와 \(x_j\)의 유사도
- \(L(r_{ij},g(x_i,x_j;w))\): Label \(r_{ij}\)와 추정된 유사도 \(g(x_i,x_j;w)\)간의 loss
- \(w\): 모델 파라미터
따라서 Loss는 다음과 같이 정의됩니다. \[L(r_{ij},g(x_i,x_j;\text{w})) = -r_{ij}log(g(x_i,x_j;\text{w})) - (1-r_{ij})log(1-g(x_i,x_j;\text{w})). \tag{2}\]
Binary Cross Entropy Loss와 동일한 구조입니다. 그러나 상단의 수식에는 두 가지 문제가 있습니다.
- 추정된 유사도 \(g(x_i, x_j ;w)\)만을 가지고 \(x_i\)와 \(x_j\)의 클러스터를 알 수 없음
- 이미지 클러스터링 과정에서 y 즉 \(r_{ij}\)를 알 수 없음
Section 3.2 및 3.3에서 두 가지 문제의 해결방법에 대한 설명을 이어가겠습니다.
Label Fetures under Clustering Constraint
이미지 쌍의 유사도를 추정하기 위해 label features \(L = {\lbrace l_i \in \Bbb{R}^k \rbrace}_{i=1}^n\)가 도입되었습니다. \(l_i\)는 이미지 \(x_i\)의 k-dimensional label feature를 나타냅니다. 유사도 \(g(x_i, x_j ;w)\)는 두 label features 간의 cosine distance로 정의되었습니다. 또한, 이미지 클러스터링에 유용한 feature representation을 학습하기 위해 label features에 clustering constraint를 추가하였습니다. \[\forall \, i, \, \lVert l_i \rVert_2 = 1, \text{and} \, l_{ih} \geq 0, \, h = 1,\dots,k, \tag{3}\]
- \(l_i\): 이미지 \(x_i\)의 k-dimensional label feature
- \(\lVert \cdot \rVert_2\): L2-norm
- \(l_{ih}\): Label feature \(l_i\)의 h번째 요소
즉 i 개의 모든 이미지 데이터에서 각 label features의 L2 norm이 1이 되도록 제약을 둔 것입니다.
벡터의 L2 norm을 1로 만들려면 L2 normalization을 하면 됩니다. 따라서, 저는 이 제약을 L2 normalizaion 했다는 것으로 해석하였습니다. L2 norm을 하게 되면 \(\lVert l_i \rVert_2 = 1\) 이 되면서 본 연구에서 도입한 clustering constraint를 따르게 됩니다. L2 normalization에 대한 설명은 이전 포스팅 L1 and L2 Norm / Normalization / Regularization을 참고하시길 바랍니다. 머신러닝의 전처리에서 정규화(normalization)를 하는 것과 같이, L2 normalization은 데이터의 값을 scaling 하여 원활한 학습에 도움을 줍니다. 또한, 데이터의 값을 0 ~ 1 사이의 값으로 만들어줌으로써 \(l_i \cdot l_j <= 1\)이 되고 그래야 식 (2)의 \(log(1-g(x_i,x_j;w))\) 값도 0 ~ 1 사이의 값이 될 수 있습니다.
i 개의 모든 이미지 데이터에서 각 label features의 L2 norm은 1이므로(\(\forall i, \, \lVert l_i \rVert_2 = 1\)), cosine similarity \(g(x_i, x_j ;w)\)는 다음과 같이 계산할 수 있습니다. \[g(x_i,x_j;\text{w}) = f(x_i;\text{w}) \cdot f(x_j;\text{w}) = l_i \cdot l_j, \tag{4}\]
- \(f_\text{w}\): 입력 이미지를 label features로 매핑해주는 mapping function
- 연산자 \(\cdot \,\): 내적
즉, 두 이미지간의 유사도 \(g(x_i, x_j ;w)\)는 label features 간의 내적으로 정의할 수 있습니다.
원래 cosine similarity는 두 vector의 내적을 각 L2 norm의 곱으로 나누어야 합니다. \(cosine \, similarity := cos(\theta) = \frac{A \cdot B}{\lVert A \rVert \lVert B \rVert}\)
그러나 본 연구에서는 clutering constraint 즉 L2 norm이 1이 되도록 만들어주었기에 label features 간의 내적이 곧 cosine similarity가 됩니다.
따라서 DAC 모델은 다음과 같이 재구성할 수 있습니다. \[\begin{align} & \min\limits_\text{w} E(\text{w}) = \sum_{i,j} L(r_{ij},l_i \cdot l_j), \\ \tag{5} \\ \ & s.t. \forall \, i, \, \lVert l_i \rVert_2 = 1, \text{and} \, l_{ih} \geq 0, \, h = 1,\dots,k. \end{align}\]
Labeled Training Samples Selection
\(\sum_{i,j} L(r_{ij},g(x_i,x_j;\text{w}))\)에서 \(x_i\)와 \(x_j\)가 같은 클러스터 일 때 \(r_{ij} = 1\)로 \(x_i\)와 \(x_j\)가 다른 클러스터 일 때 \(r_{ij} = 0\)으로 나타내기로 하였습니다. 그러나 실제로는 \(r_{ij}\)의 값을 알 수 없습니다. 따라서 labeled training smaples을 선택하는 전략이 필요합니다. 특히 ConvNets의 경우 두 가지 관찰 결과가 있습니다.
- 사전에 학습된 ConvNets은 이미지의 high-level features를 생성할 수 있습니다.
- 랜덤으로 초기화된 ConvNets은 랜덤으로 초기화된 필터가 edge detectors와 같은 역할을 하기 때문에 이미지의 low-level features도 포착할 수 있습니다.
따라서 All-ConvNets을 사용하여 \(f_w\)을 구현하고 생성된 labeled features를 기반으로 labeled training samples을 선택합니다.
- \(\lambda\): Training samples의 선택을 제어하기 위한 adaptive parameter
- \(u(\lambda)\): Similar labeled samples을 선택하기 위한 thresholds
- \(l(\lambda)\) Disimilar labeled samples을 선택하기 위한 thresholds
- \(None\): Sample \((x_i, x_j, r_{ij})\)이 학습에서 생략되었음을 의미
클러스터링 과정에서 samples이 점점 더 많이 선택되도록 파라미터 \(\lambda, u(\lambda), l(\lambda)\)를 조절하였습니다. 먼저, 대략적인 클러스터의 패턴을 찾기 위해 가능성이 높은 “쉬운” 샘플을 training samples로 선택합니다. 다음으로 클러스터링이 진행되면서 학습된 ALL-ConvNets을 사용하여 더 효과적인 label features를 추출할 수 있으며, 더 정교한 클러스터의 패턴을 찾기 위해 더 많은 샘플이 점점 더 추가됩니다. 구체적으로 \(\lambda\)는 클러스터링 과정에서 점차 증가하며, \(u(\lambda) \varpropto -\lambda, \, l(\lambda) \varpropto \lambda, l(\lambda) \le u(\lambda)\)가 영구적으로 충족됩니다. \(u(\lambda) = l(\lambda)\)는 만약 모든 샘플이 학습에서 사용되는 경우에만 충족됩니다.
점진적으로 샘플의 수를 증가시키기 위해, \(l_i \cdot l_j \geq u(\lambda)\)에서 threshold \(u(\lambda)\)는 낮아져야 하며 \(l_i \cdot l_j \lt l(\lambda)\)에서 threshold \(l(\lambda)\)은 높아져야 합니다. 따라서, \(u(\lambda)\)는 \(\lambda\)와 반비례 관계가 되고 \(l(\lambda)\)은 \(\lambda\)와 비례 관계가 되며 \(l(\lambda) \le u(\lambda)\)가 영구적으로 충족됩니다.
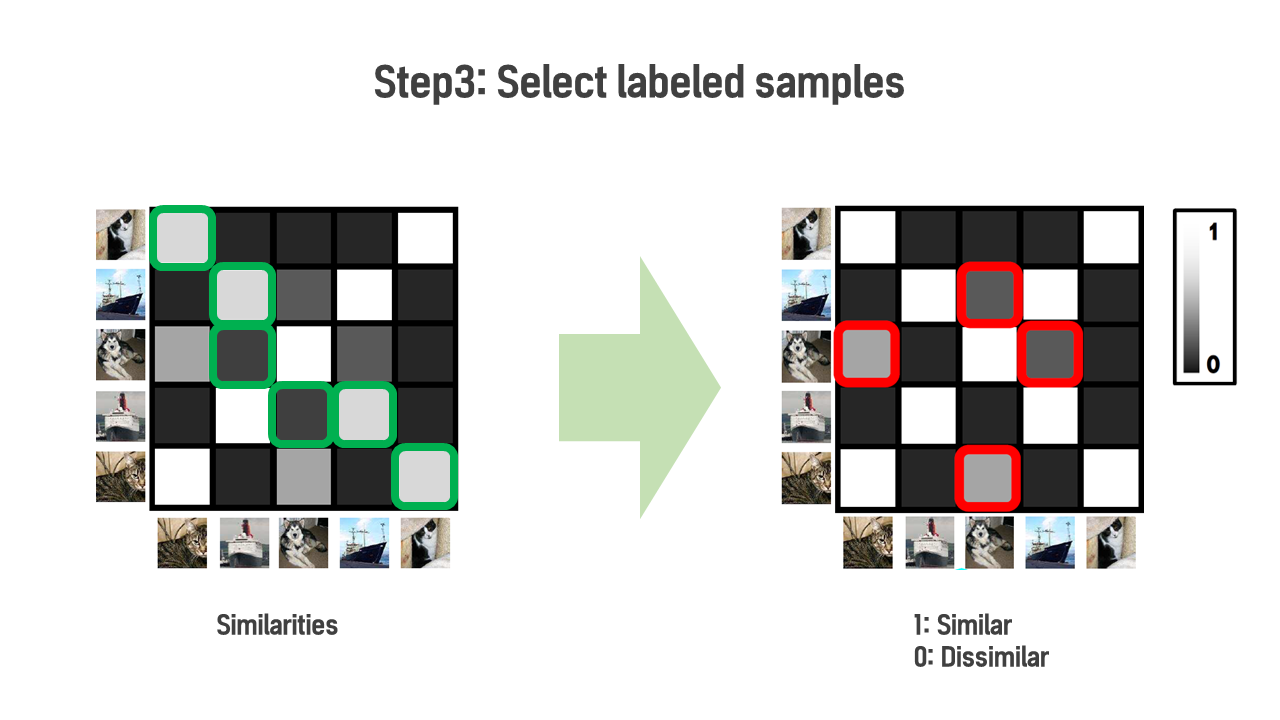
Step 3. Select labeled samples
상단의 그림은 DAC의 흐름도에서 Step3. Select labeled samples 부분을 나타냅니다. 왼쪽 그림은 계산된 cosine similariries로 녹색 박스를 보시면 옅은 회색 또는 진한 회색으로 0~1 사이의 값인 것을 알 수 있습니다. 그러나, Eq.(6)번을 통해 \(u(\lambda)\) 보다 큰 것은 1로, \(l(\lambda)\)보다 작은 것은 것은 0으로 바뀐 것을 오른쪽 그림에서 확인하실 수 있습니다. 빨간색 박스의 샘플들은 “otherwise”에 속하여 labeled training samples에서 제외되었습니다.
지금까지 Section 3.1에서 2가지 문제를 다루었습니다. DAC 모델은 다음과 같이 작성할 수 있습니다. \[\begin{align} & \min_{\text{w}, \lambda}E(\text{w}, \lambda) = \sum_{i,j}v_{ij}L(r_{ij}, l_i \cdot l_j) + u(\lambda) - l(\lambda), \\ \ & s.t. \, l(\lambda) \le u(\lambda), \\ \ & \qquad v_{ij} \in \{0, 1\}, \: i, \, j = 1, \dots, n, \\ \tag{7} \\ \ & \qquad \forall \, i, \, \lVert \, l_i \, \rVert_2 = 1, \text{and} \, l_{ih} \geq 0, \: h = 1, \dots, k, \\ \ & \qquad r_{ij} := \begin{cases} \enspace 1, \enspace \text{if } l_i \cdot l_j \geq u(\lambda), \\ \enspace 0, \enspace \text{if } l_i \cdot l_j \lt l(\lambda), \quad i, \; j=1, \dots, n, \\ \enspace \text{None}, \enspace \text{otherwise}, \end{cases} \end{align}\] \[v_{ij} := \begin{cases} \enspace 1, \enspace \text{if } r_{ij} \in \{0, 1\}, \\ & i, \, j = 1, \dots, n, \tag{8} \\ \enspace 0, \enspace \text{otherwise }, \\ \end{cases}\]