[Deep learning] Similarity measure
머신러닝에서 사용되는 데이터 거리 측정 방법
머신러닝에서 데이터간의 거리를 구하는 방법에 대해서 알아보고자 합니다. 설명에 앞서 Mahmoud Harmouch님의 블로그를 번역하였음을 밝힙니다.
Overview
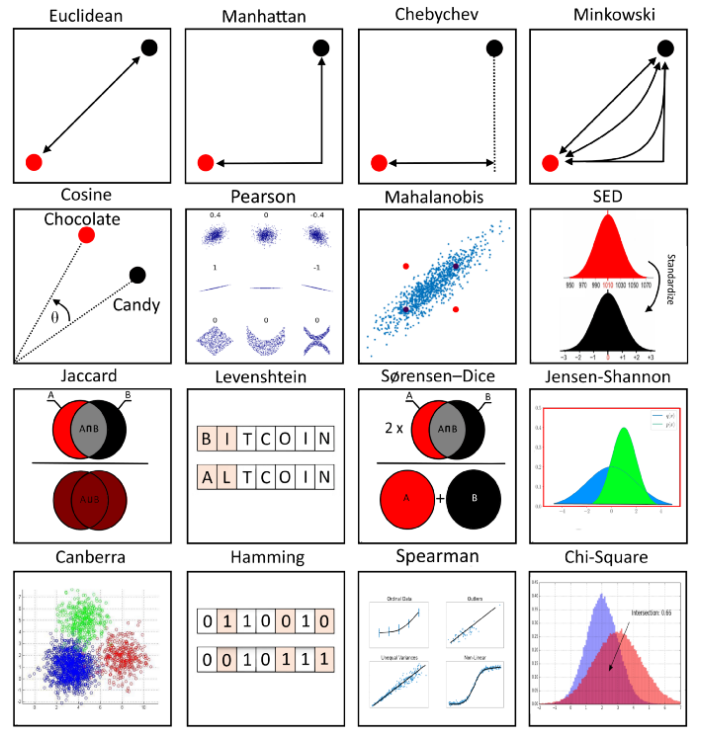
Various ML metrics(Source: Towards Data Science).
Introduction
머신러닝에서 유사도 측정(similarity measure)은 개별 데이터 간의 관련성(relation)을 측정하는 방법입니다. 반면에 비유사도 측정(dissimilarity measure)은 개별 데이터들이 얼마나 구별되는지(distinct)를 나타냅니다. 유사도 측정이라는 용어는 머신러닝에서 다방면으로 사용됩니다.
- Clustering: 비슷한 데이터들끼리 하나의 클러스터로 묶음
- Classification: 특징의 유사성(features’s similarity)에 따라 데이터 분류(e.g., KNN)
- Anomaly detection: 다른 데이터들과 유사하지 않은 이상값 탐지
일반적으로 유사도 측정은 숫자 값(numerical value)으로 표현됩니다. 데이터들 간의 관련성이 높아질 경우 값도 커집니다. 가끔 변환되어 0과 1사이의 숫자로 표현되기도 합니다. 0은 낮은 유사도, 즉 유사하지 않음을 뜻하며 1은 높은 유사도, 즉 매우 유사함을 의미합니다. 예를 들어, 하나의 input feature만을 갖고 있는 데이터 포인트 A, B, C가 있습니다. Input feature가 한 개이므로 각 데이터는 한 축에 하나의 값을 가질 수 있습니다. 그 축을 x축이라고 할 때 A(0.5), B(1), C(30)에서 두 점을 살펴보겠습니다. 쉽게 알 수 있듯이, A와 B는 C와 비교할 때 서로 가깝습니다. 따라서, A와 B의 유사도는 A와 C 또는 B와 C의 유사도보다 큰 값을 가집니다. 다시 말해 데이터 간의 거리가 가까울수록, 유사도는 커집니다.
Metric
주어진 거리(distance)는 다음 네 가지 조건을 충족하는 경우에만 지표(metric)로 사용할 수 있습니다.
- Non-negativity: d(p, q) ≥ 0, for any two distinct obeservations p and q.
\(\to\) 두 지점 p와 q 사이의 거리는 음수가 되면 안됩니다. - Symmetry: d(p, q) = d(q, p) for all p and q. \(\to\) 두 지점 p와 q 사이의 거리는 q와 p 사이의 거리와 동일해야 합니다.
- Triangle Inequality: d(p, q) ≤ d(p, r) + d(r, q) for all p, q, r. \(\to\) 삼각 부등식(triangle inequality)에 따라 두 변의 합이 나머지 한 변보다 커야 힙니다.
- d(p, q) = 0 if only if p = q. \(\to\) p와 q가 같을 때, p와 q 사이의 거리는 0이어야 합니다.
거리 측정은 주어진 데이터들 간의 비유사도를 측정하는 k-nearest neigbor(K-NN) 알고리즘과 같은 분류(classification)의 기본적인 원칙입니다. 또한, 어떤 거리 지표(distance metric)를 사용하느냐에 따라 분류기의 성능은 크게 달라집니다. 따라서, 객체 간의 거리를 구하는 방식은 분류기 알고리즘 성능에 중요한 역할을 합니다.
Distance function
거리를 측정하기 위해 사용되는 기술은 작업 중인 상황에 따라 상이합니다. 예를 들어, 일부 영역에서는 유클리드 거리(Euclidian distance)가 거리 계산에 적절하고 유용할 수 있지만, 다른 영역에서는 코사인 거리(Cosine distance)와 같은 정교한 방식이 필요할 수 있습니다. 따라서, 데이터 포인트 간의 거리를 계산하는 다양한 방법을 소개하고자 합니다.
L2 norm, Euclidean distance
유클리드 거리(Euclidean distance)는 numeric attributes 또는 features와 같이 수치로 표현된 자료에서 가장 흔히 사용되는 거리 함수이며 수식은 다음과 같이 정의됩니다. \[\begin{aligned} d(P,Q) = \lVert P - Q \rVert_0 &= \sqrt{\sum_{i=1}^n (p_i - q_i)^2} \\ &= \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2 + \dots + (p_n - q_n)^2} \end{aligned}\]
where:
\(P = (p_1,p_2,\dots,p_n),\) and \(Q = (q_1,q_2,\dots,q_n)\)
아시다시피 유클리드 거리 측정법은 대칭성(symmetry), 미분가능성(differentiability), 볼록성(convexity), 구형성(sphericity) 등 잘 알려진 속성을 나타냅니다.
2차원 공간에서는 다음과 같이 표현할 수 있습니다. \[\begin{aligned} d(P,Q) = \lVert P - Q \rVert_0 &= \sqrt{\sum_{i=1}^2 (p_i - q_i)^2} \\ &= \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2} \end{aligned}\]
where:
\(P = (p_1,p_2),\) and \(Q = (q_1,q_2)\)
해당 식은 직각삼각형의 빗변의 길이를 구하는 공식과 동일합니다.
또한, 유클리드 거리는 앞서 말씀드린 4가지 기준을 충족하기에 지표(metric)라고 할 수 있습니다.
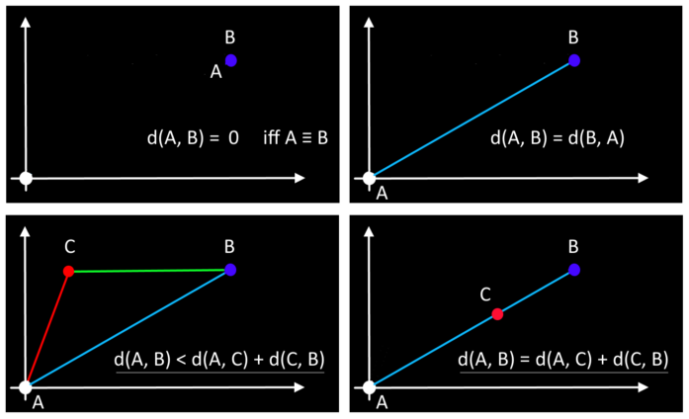
The Euclidean distance satisfies all the conditions for being a metric(Source: Towards Data Science).
또한, 해당 공식을 통해 계산된 거리는 두 점 사이의 가장 짧은 거리를 나타냅니다. 다시 말해, A 지점에서 B 지점으로 가는 최단 경로입니다.

The Euclidean distance is the shortest path(Source: Towards Data Science).
따라서, 장애물이 없는 상태에서 두 점 사이의 거리를 계산해야 할 때 유클리드 거리가 유용할 수 있습니다. 분류 알고리즘 중 하나인 KNN 알고리즘을 기반으로 유클리드 거리를 사용하여 분류 과정을 설명드리겠습니다. 예제 데이터로는 Scipy 패키지에 있는 iris dataset을 사용하고자 합니다.
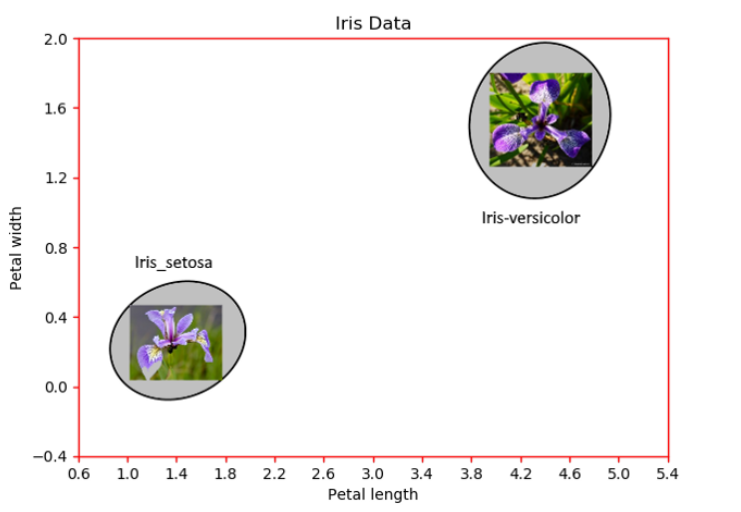
Iris dataset for two types of flowers in two features’ space(Source: Towards Data Science)
Iris dataset은 붓꽃의 3가지 종(Iris-Setosa, Iris-Versicolor, Iris-Virginica)에 대해 4가지의 features(꽃받침 길이, 꽃받침 너비, 꽃잎 길이, 꽃잎 너비)가 있는 데이터입니다. 따라서 각 데이터 포인트를 표현할 수 있는 4차원 공간이 있습니다. 원활한 설명을 위하여 2가지의 features 꽃잎 길이(petal length)와 꽃잎 너비(petal width)만 사용하고, label도 2가지 Iris-Setosa, Iris-Versicolor만 사용하겠습니다. 이런 식으로 x축과 y축에 각각 petal length와 petal width를 나타내는 2차원 공간의 데이터 포인트를 시각화 할 수 있습니다.
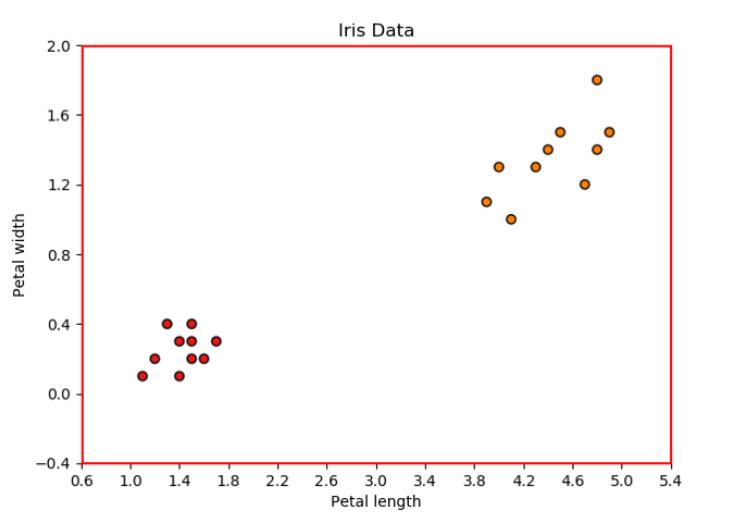
Training dataset(Source: Towards Data Science).
각 데이터 포인트는 Iris-Setosa 또는 Iris-versicolor에 속하므로, KNN 분류를 위한 데이터셋으로 사용할 수 있습니다. 따라서 2개의 input features와 20개의 데이터 포인트를 가지고 KNN(k = 4)을 학습한다고 가정해 보겠습니다.
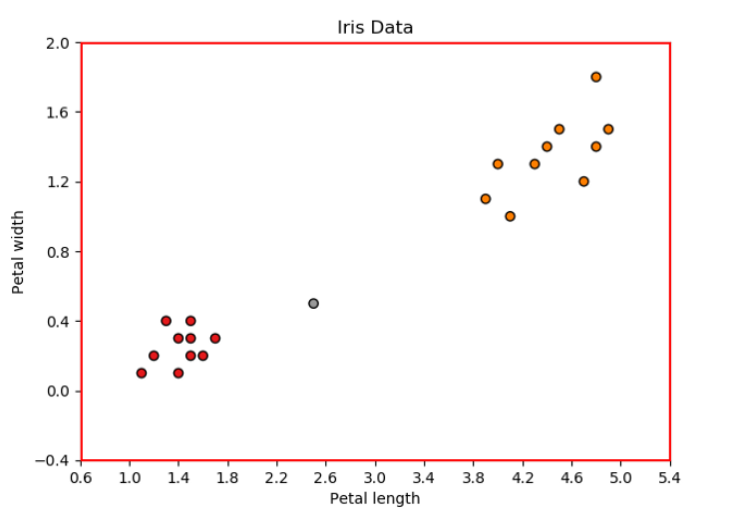
Predict the label for a new data point(Source: Towards Data Science).
KNN은 학습을 통해 새로운 데이터 포인트를 분류할 수 있습니다. 모델은 새로운 데이터 포인트를 어떻게 분류할까요?
KNN 알고리즘은 새로운 데이터로부터 거리가 가까운 k개의 다른 데이터의 label을 참고하여, k개의 데이터 중 가장 빈도 수가 높에 나온 label로 새로운 데이터를 분류합니다. 이때 데이터 간의 거리를 측정하기 위해 유클리드 거리를 사용할 수 있습니다.
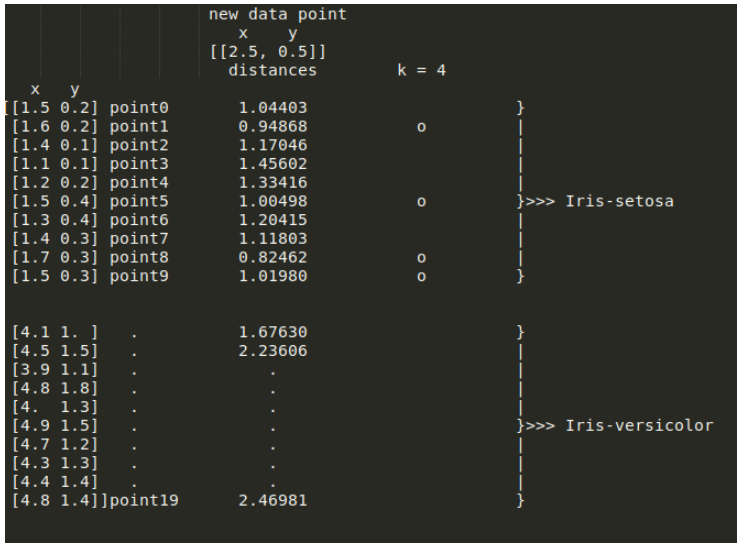
Source: Towards Data Science
새로운 데이터에서 training data의 각 지점까지의 유클리드 거리를 계산한 결과입니다. k = 4 이므로, KNN은 새로운 데이터에서 가장 가까운 4개의 지점을 선택해야 합니다. 위 그림에서 point1, point5, point8, point9에서의 거리가 가장 짧은 것을 알 수 있습니다. 해당 지점들을 그래프로 그려보면 다음과 같습니다.
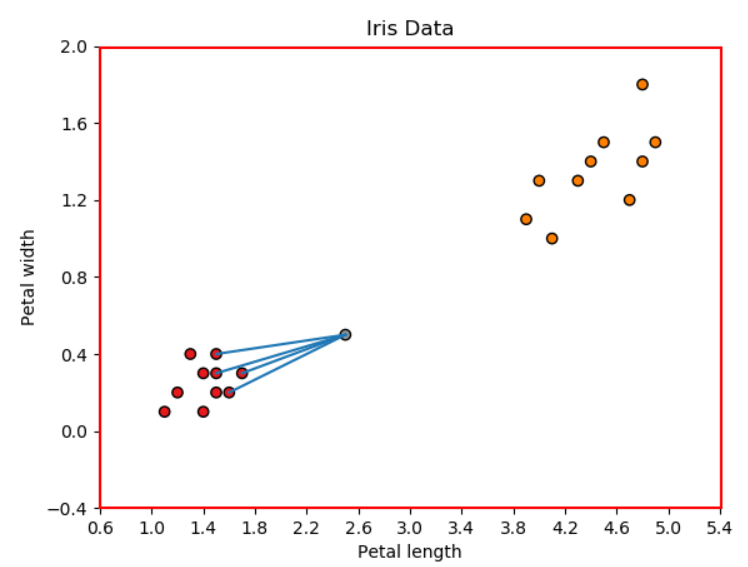
Four neighbors voted for Iris-Setosa(Source: Towards Data Science).
따라서 새로운 데이터는 Iris-Setosa로 분류되었습니다.
그러나 도메인에 따라 사용되는 거리 측정 방법이 다르며, 유클리드 거리는 직선이 아닌 곡선을 따르는 경로에서는 유용하지 않을 수 있습니다.
Squared Euclidean distance
유클리드 제곱 거리(Squared Euclidean Distance, SED)는 유클리드 거리의 제곱과 같습니다. 그러므로, 제곱근 함수를 사용할 필요가 없으며 계산량을 줄일 수 있습니다. \[\begin{aligned} d(P,Q) &= \sum_{i=1}^n (p_i - q_i)^2 \\ &= (p_1 - q_1)^2 + (p_2 - q_2)^2 + \dots + (p_n - q_n)^2 \end{aligned}\]
where:
\(P = (p_1,p_2,\dots,p_n),\) and \(Q = (q_1,q_2,\dots,q_n)\)
L1 norm, Manhattan distance, City block, taxicab distance
맨해튼 거리(Manhattan distance)는 도시에서 두 streets 간의 거리를 측정할 때 매우 유용합니다.
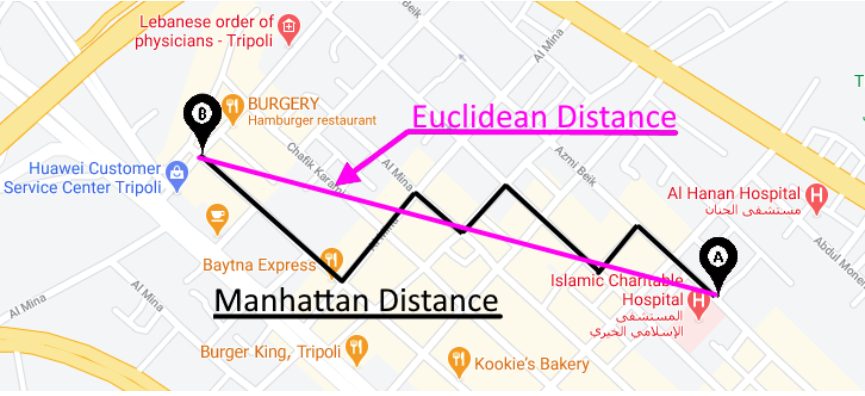
Manhattan distance in real world(Source: Towards Data Science).
예를 들어, 상단의 그림에서 A지점과 B지점 사이의 거리는 대략 4 blocks입니다. 맨해튼 거리는 도시와 같이 일직선으로 가지 못하는 곳에서 출발지와 목적지 사이의 거리를 계산하기 위해 만들어졌습니다. 다라서 이름이 City Block입니다. 물론, A지점에서 B지점까지의 거리도 유클리드로 계산할 수 있지만 유용하지 않습니다. 맨해튼 거리는 이동 시간이나 운전 시간을 추정할 때 유용하게 사용됩니다. 따라서 거리를 어떻게 정의하고 사용할 수 있는지에 따라 상황이 달라집니다.
n-차원 공간에서 맨해튼 거리는 다음과 같이 표현됩니다. \[\begin{aligned} d(P,Q) = \lVert P - Q \rVert_1 &= \sum_{i}^n \lvert p_i - q_i \rvert \\ &= \lvert p_1 - q_1 \rvert + \vert p_2 - q_2 \rvert + \dots + \lvert p_n - q_n \rvert \end{aligned}\]
where:
\(P = (p_1,p_2,\dots,p_n),\) and \(Q = (q_1,q_2,\dots,q_n)\)
2차원 공간에서는 다음과 같이 표현할 수 있습니다. \[\begin{aligned} d(P,Q) = \lVert P - Q \rVert_1 &= \sum_{i}^2 \lvert p_i - q_i \rvert \\ &= \lvert p_1 - q_1 \rvert + \vert p_2 - q_2 \rvert \end{aligned}\]
where:
\(P = (p_1,p_2),\) and \(Q = (q_1,q_2)\)
앞선 유클리드 거리를 기반으로 KNN을 적용한 것과 같이, 맨해튼 거리로 새로운 데이터에서 training data 간의 거리를 계산하면 다음과 같은 결과를 얻을 수 있습니다.
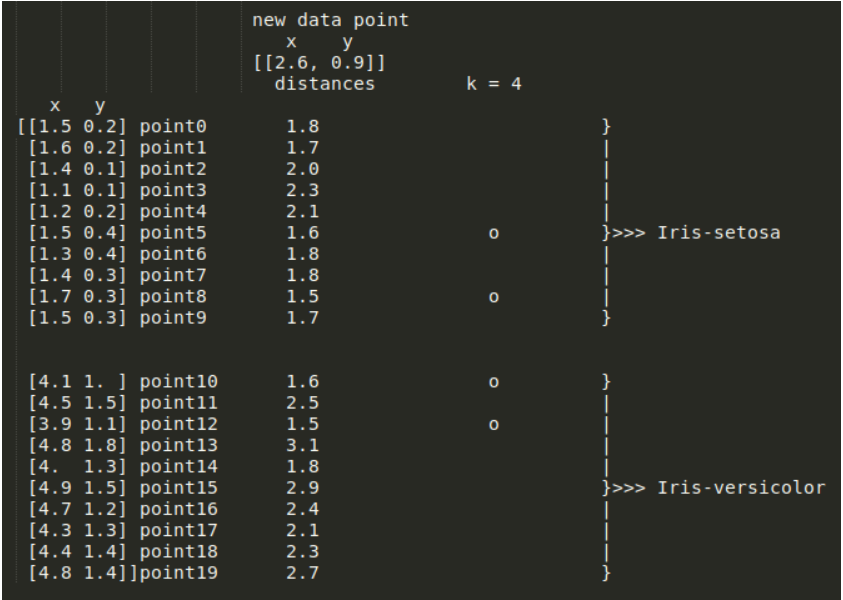
KNN classification using Manhattan distance(Source: Towards Data Science).
위의 그림에서 확인할 수 있듯이, 2개의 points는 새로운 데이터를 Iris-Setosa로 투표했고, 나머지 2개의 points는 Iris-Versicolor로 투표했습니다. 이는 동점을 의미합니다.
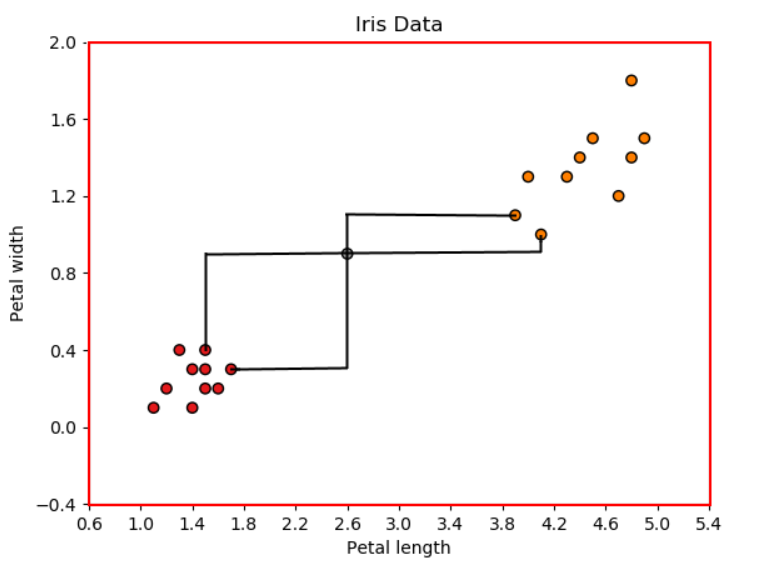
Manhattan distance: a tie(Source: Towards Data Science)!
이런 문제에서는 k의 값을 변경함으로써 즉 k의 값을 1만큼 늘리거나 줄여서 해결할 수 있습니다. 그러나, k의 값에 따라 KNN의 성능은 달라질 수 있습니다.
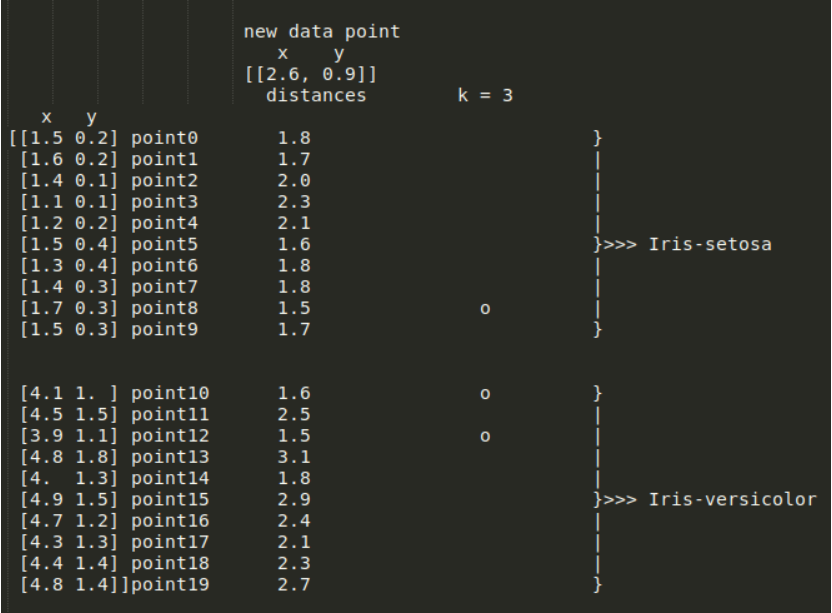
Decreasing k by one(Source: Towards Data Science).
예를 들어, k=3으로 바꾸면 새로운 데이터는 Iris-Versicolor로 분류됩니다.
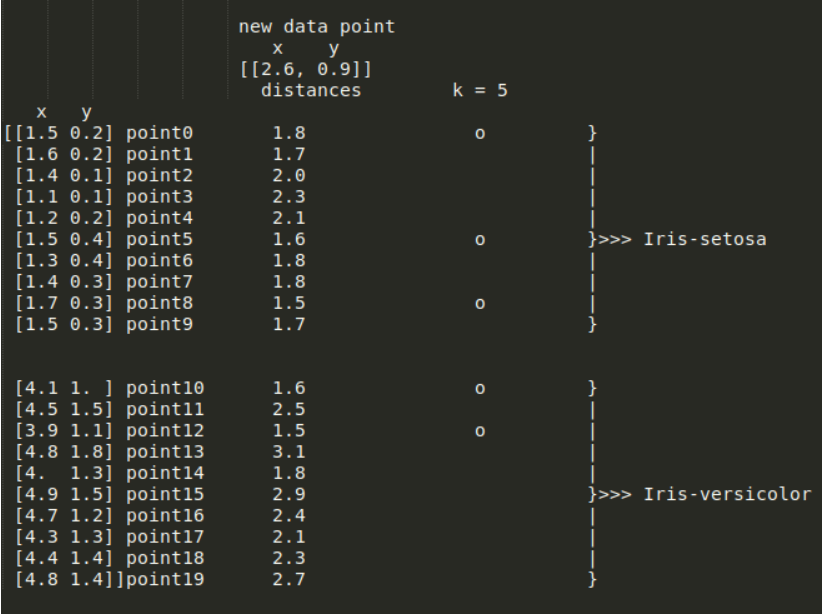
Increasing k by one(Source: Towards Data Science).
그러나 k=5로 바꾸면 새로운 데이터는 Iris-Setosa로 분류됩니다. 따라서 k의 값을 증가시킬 것인지 감소시킬 것인지는 사용자에게 달려있습니다. 만약, 새로운 차원(dimension) 또는 feature를 추가할 수 있다면 동일한 k값으로도 다른 결과를 야기할 수 있습니다. Iris dataset에서 꽃받침 너비(sepal width)를 새로운 차원으로 추가하면 다음과 같은 결과가 나옵니다.
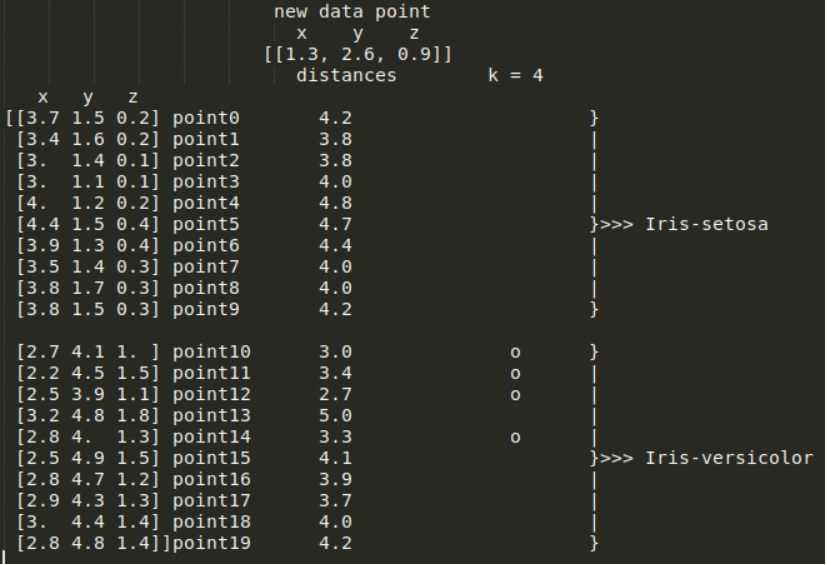
Adding a new feature to the model(Source: Towards Data Science).
새로운 데이터는 Iris-Versicolor로 분류됩니다.
각 feature를 3d 공간에서 표현하면 다음과 같습니다.
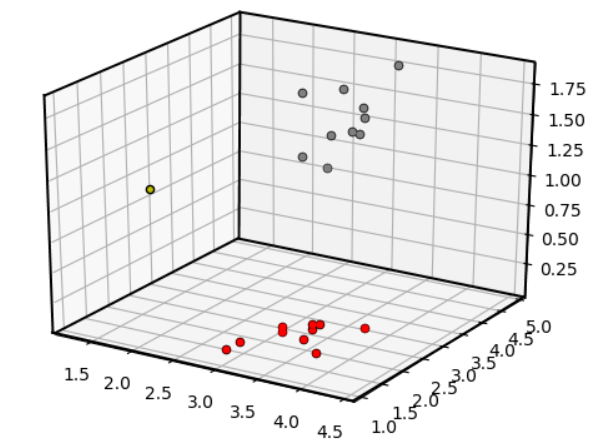
A 3-D plot of Iris dataset(Source: Towards Data Science).
유클리드 및 맨해튼 거리는 정규화(regularization)에서도 사용됩니다. L1 및 L2 Regularization에 대한 자세한 설명은 L1 and L2 Regularization을 참고하시길 바랍니다.
Canberra distance
References
[1] Towards Data Science, 17 types of similarity and dissimilarity measures used in data science. [Online]