[Deep learning] L1 and L2 Norm / Normalization / Regularization
L1 및 L2 Norm, Normalization, Regularization에 대한 설명
L1 및 L2 Norm에서 대해서 살펴보고 나아가 L1 및 L2 Norm을 활용한 Normalization과 Regularization를 알아보고자 합니다.
Overview
| L1 Norm \({\lVert w \rVert}_1 = \lvert w \rvert\) | L2 Norm \(\frac{1}{2} {\lVert w \rVert}^2 = \frac{1}{2}w^2\) |
|---|---|
| - Manhattan distance | - Euclidean distance |
| - Lasso Regression - 가중치의 값을 완전히 0으로 축소하는 경향 - 중요한 특징을 선택하는 feature selection 효과 - Convex하여 global optimum에 수렴 가능 - Features의 영향력 편차가 큰 경우 사용 | - Ridge Regression - 가중치의 값을 0에 가까운 수로 축소하는 경향 - 모델의 전반적인 복잡도를 감소시키는 효과 - Convex하여 global optimum에 수렴 가능 - 전반적으로 features가 비슷한 수준으로 성능에 영향을 미치는 경우 사용 |
L1, L2 Norm
Norm은 벡터의 크기를 측정하는 방법이며, 두 벡터 사이의 거리를 측정하는 방법이기도 합니다. 가장 일반적으로 사용되는 vector norms은 \(p\text{-}norms\)또는 \(l_p\text{-}norms\) 계열에 속하며 다음과 같이 정의됩니다. \[\lVert \mathbf{x} \rVert_p = \Bigg( \sum_{i=1}^n \lvert x_i \rvert^p \Bigg)^{1/p}\]
- \(p\): Norm 의 차수
- \(n\): 해당 벡터의 원소 수
\(p = 1\) 이면 \(l_1\text{-}norm, \; p = 2\) 이면 \(l_2\text{-}norm\) 이 됩니다.
L1 Norm \[\begin{aligned} \lVert \mathbf{x} \rVert_1 &= \sum_{i=1}^n \lvert x_i \rvert \\[0.5em] &= \lvert x_1 \rvert + \lvert x_2 \rvert + \dots + \lvert x_n \rvert \end{aligned}\]
각 원소들의 절댓값의 합으로 표현되며 Manhattan norm이라고도 합니다.
L2 Norm \[\begin{aligned} \lVert \mathbf{x} \rVert_2 &= \Bigg( \sum_{i=1}^n \lvert x_i \rvert^2 \Bigg)^{1/2} \\[0.5em] &= \sqrt{x_1^2 + x_2^2 + \dots + x_n^2} \\[0.5em] &= \sqrt{\mathbf{x^T}\mathbf{x}} \end{aligned}\]
각 원소의 제곱의 합을 루트로 씌워준 값으로 Euclidean norm이라고도 합니다. 2차원에서 직각삼각형의 빗변의 길이를 구하는 공식과 동일하며 해당 공식을 통해 계산된 거리는 두 점 사이의 가장 짧은 거리를 나타냅니다.
L1 Norm vs L2 Norm
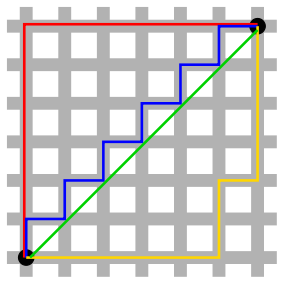
Manhattan versus Euclidean distance(Source: Wikipedia).
검정색의 두 점 사이의 거리를 L1 및 L2 Norm으로 나타낼 수 있습니다.
- L1 Norm 은 빨간색, 파란색, 노란색 선으로 표현될 수 있으며 모두 최단 경로 길이가 12로 동일합니다.
- L2 Norm 은 오직 초록색 선으로만 표현 가능합니다.
Normalization
정규화(Normalization)는 데이터의 scale을 조정하는 작업입니다. 즉, 다양한 값의 데이터를 0 ~ 1 사이의 값으로 조정하는 것을 뜻합니다. 데이터의 scale 범위가 크면(상한값과 하한값의 범위가 매우 큰 경우), 과적합(overfitting)이 발생하기 쉬우며 local optimum에 빠질 가능성어 정규화가 자주 사용됩니다. 대표적으로 머신러닝에서는 Min-max scale이 주로 사용되지만, 간혹 딥러닝에서는 L1 및 L2 normalization이 사용됩니다.
L1 Normalization \[l_1(x_i) = \frac{x_i}{\sum_{j=1}^n \lvert x_j \rvert}\]
머신러닝 라이브러리 scikit-learn을 통해 쉽게 L1 및 L2 Normalization을 할 수 있습니다.
import numpy as np
from sklearn import preprocessing
# 2 samples, with 3 dimensions.
# The 2 rows indicate 2 samples.
# The 3 columns indicate 3 features for each sample.
X = np.asarray([[-1,0,1],
[0,1,2]], dtype=np.float) # Float is needed.
# Before-normalization.
print(X)
# Output,
# [[-1. 0. 1.]
# [ 0. 1. 2.]]
# l1-normalize the samples (rows).
X_normalized_l1 = preprocessing.normalize(X, norm='l1')
# After normalization.
print(X_normalized_l1)
# [[-0.5 0. 0.5]
# [ 0. 0.3 0.67]]
L2 Normalization \[l_2(x_i) = \frac{x_i}{\sqrt{\sum_{j=1}^n x_j^2}} = \frac{x_i}{\sqrt{x^Tx}}\]
X = np.asarray([[-1,0,1],
[0,1,2]], dtype=np.float) # Float is needed.
# Before-normalization.
print(X)
# Output,
# [[-1. 0. 1.]
# [ 0. 1. 2.]]
# l2-normalize the samples (rows).
X_normalized_l2 = preprocessing.normalize(X, norm='l2')
# After normalization.
print(X_normalized_l2)
# Output,
# [[-0.70710678 0. 0.70710678]
# [ 0. 0.4472136 0.89442719]]
Regularization
 \[W_{new} = W_{old} - (LR * \frac{\partial{Cost}}{\partial{W}})\]
\[W_{new} = W_{old} - (LR * \frac{\partial{Cost}}{\partial{W}})\]
정규화(regularization)는 predict function에 복잡도를 조정하기 위해 weights에 페널티를 주는 작업입니다. Train data에 과적합(overfitting)되는 것을 방지하고 모델의 강건함을 개선하기 위해 사용됩니다. 다시 말해 Loss function에 regularization을 더하여 Train data에 편중되어 학습하는 것을 방지합니다. 따라서, Loss + Regularization은 제약 조건이 있는 상태의 최적화 문제입니다.
정규화는 일반화(genenralization)를 위하여 제약 조건을 추가하는 기법으로, Loss 값의 감소를 기대하면 안됩니다.
L1 Regularization \[\begin{align} Cost &= \text{Loss + L1 Weight Penalty} \\ &= \sum_{i=1}^M (y_i - \sum_{j=1}^N x_{ij}w_j)^2 + \color{red} \lambda \sum_{j=1}^N \lvert w_j \rvert \end{align}\]
\(\lambda\)는 정규화 비중을 얼마나 줄 것인지 정하는 계수입니다. 0에 가까울수록 정규화의 효과는 사라집니다. K-fold cross validation을 통해 적절한 \(\lambda\) 값을 찾을 수 있습니다.
L1 regularization의 경우 Cost 함수를 가중치로 미분하게 되면 regularization term의 \(w_j\)들은 모두 1까지 미분되어 결국 \(\lambda\)라는 상수항만 남게 됩니다. 결국 고정된 상수값 \(\lambda\)가 모든 항에 대해 공평하게 빠지면서, **작은 가중치들은 0이 되고 중요한 가중치만 남게 됩니다. 따라서 feautre 수가 줄어들어 과적합을 방지**할 수 있습니다. L1 regularizatoion을 사용하는 선형 회귀 모델을 Lasso model이라고 합니다.
L2 Regularization \[\begin{align} Cost &= \text{Loss + L2 Weight Penalty} \\ &= \sum_{i=1}^M (y_i - \sum_{j=1}^N x_{ij}w_j)^2 + \color{red} \frac{1}{2} \lambda \sum_{j=1}^N w_j^2 \end{align}\]
\(\lambda\) 앞에 있는 \(\frac{1}{2}\)은 실험적으로 알아내야 하는 값입니다. \(\frac{1}{2}\)을 하지 않는 경우도 있으며, 그 때는 regularization term으로 \(\lambda \sum_{j=1}^N w_j^2\)를 사용합니다. L2 regularization의 경우, Cost를 미분하면 \(w_j^2\)에 있는 2가 내려오면서 \(\frac{1}{2}\)이 제거되고 regularization parameter인 \(\lambda w_j\)만 남게 됩니다. 따라서 각 가중치의 크기에 비례하여 값이 빠지며, 가중치들이 완전히 0이 되지 않습니다. 가중치 업데이트는 Loss 값에 현재 가중치 크기의 일정 비율을 추가로 반영하여, 현 시점에서의 가중치를 일정 비율로 깎아 내리면서 이루어집니다. 결론적으로 L2는 크기가 큰 가중치에 대한 규제는 강하게, 작은 가중치에 대한 규제는 약하게 주게 됩니다. 이러한 성질로 L2 regularization을 가중치 감쇠(weight decay)라고도 합니다. L2 regularization을 사용하는 선형 회귀 모델을 Ridge model이라고 합니다.
Sparsity & Feature selection
- L1: 가중치의 값을 완전히 0으로 축소하는 경향 \(\to\) feature selection 가능
- L2: 가중치의 값을 0에 가까운 수로 축소하는 경향
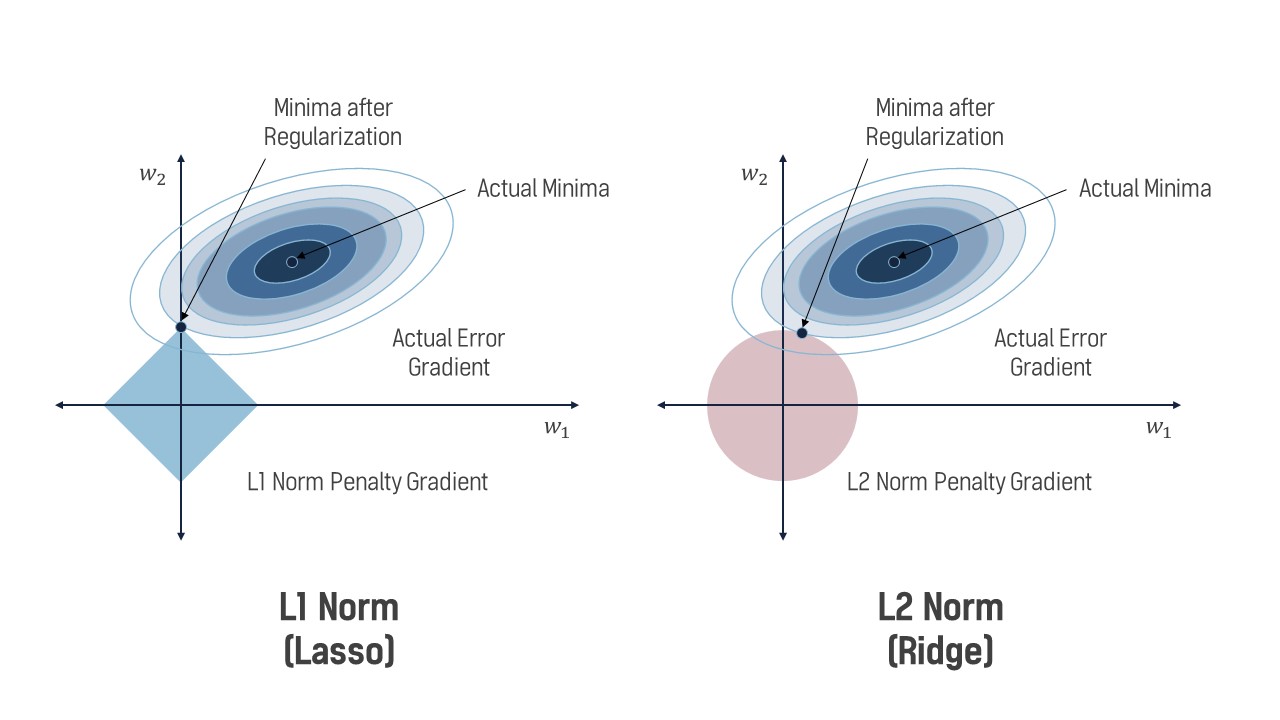
파라미터 w1, w2가 있을 때, Regularization의 분포와 Acutal Error Gradient가 한점에서 접하는 지점이 최적화된 weights의 값입니다. L1 regularization을 좌표평면에 나타내면 마름모 형태의 분포와 같고, 그림의 예제에서 \(w_1 = 0, w_2 > 0\)일 때 Loss의 최솟값을 가졌습니다. 즉 L1 regularization은 sparse vectors를 생성하는 경향이 있습니다. Sparse vector란 벡터 내 대부분의 값이 0인 벡터를 말합니다. 반면에 L2 regularization을 좌표평면에 나타내면 원의 형태와 같고, \(w_1 >0, w_2 > 0\)인 한 점에서 최적화 되었습니다. 이처럼 L2 regularization은 가중치를 0으로 만들기 보다는 0에 가까운 수로 축소합니다.
L1 regularization은 sparse vectors를 생성하는 경향으로 인해 머신러닝에서 feature selection을 가능하게 합니다. 작은 weights의 값을 0으로 만들기에 weights가 너무 많을 때는 L1을 사용하여 좀 더 중요한 weights만 남겨둘 수 있습니다.
L2 regularization은 모든 가중치를 균등하게 감소시켜 일반적으로 학습 시 더 좋은 결과를 나타냅니다.
Convexity
- L1, L2: Convex하여 global optimum에 수렴 가능
일반적으로 사용하는 Loss 함수는 미분 가능한 형태로 역전파(backpropagation)가 가능하며 convex합니다. L1 및 L2 regularization도 loss와 동일하게 covex합니다. L1은 V 형태를 띄고 L2는 U 형태를 띄기 때문입니다. 최적화 이론에서 convex + convex = convex가 성립하므로 Loss(convex) + Regularization(convex) = Loss(convex)가 성립하게 됩니다. 그러나, U 형태의 L2와 달리 L1은 V 형태이므로 미분 불가능하기에 gradient-based learning에서는 주의할 필요가 있습니다.
Summary
Norm은 주로 두 벡터 사이의 거리를 측정하기 위해서 사용되며 특히 L2 Norm이 주로 사용됩니다. Regularization의 경우 머신러닝에서는 직접 중요한 feature를 input으로 사용하므로 feature의 영향력에 따라 L1 또는 L2 regularization을 선택합니다. 반면에, 딥러닝에서는 task(e.g., regression, classification)에 있어 중요한 feature를 자동적으로 골라내야 하므로 주로 L2 regularization이 사용됩니다.
References
[1] Jinsol Kim, L1,L2 Regularization. [Online]
[2] 별보는 두더지, L1, L2 Norm & L1, L2 loss & L1, L2 규제. [Online]
[3] Seongkyun Han’s blog, L1 & L2 loss/regularization. [Online] [4] JeremyKawahara, How to normalize vectors to unit norm in Python [Online]